Understanding Tree Traversals — Hardware-Level Deep Dive
Memory layout, CPU cache performance, recursion stack overhead, and advanced optimization techniques for production systems.
Memory layout, CPU cache performance, recursion stack overhead, and advanced optimization techniques for production systems.
Author
Mr. Oz
Date
Read
12 mins
Level 3
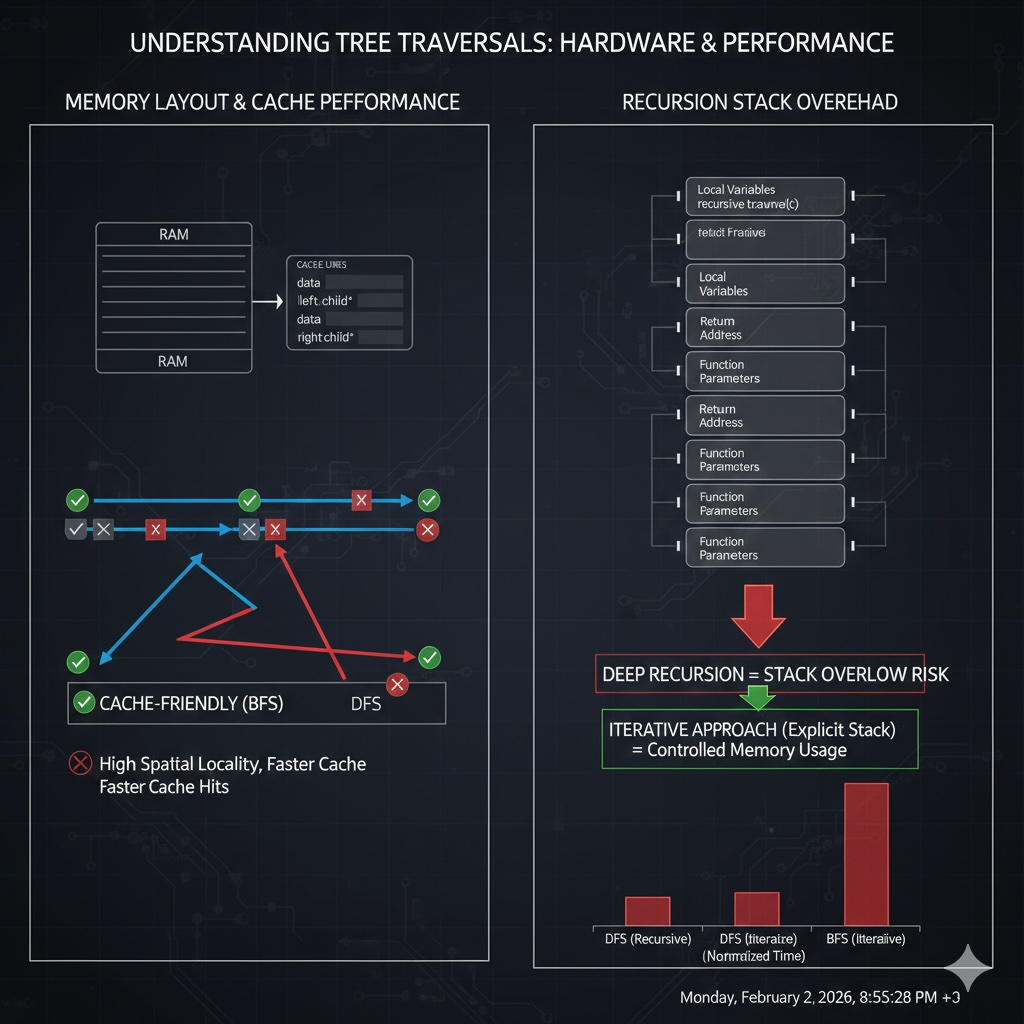
At Level 3, we look beyond correctness and examine what happens at the hardware level. How does the CPU cache interact with tree structures? Why might recursion cause stack overflow? Let's dive into memory layout, cache performance, and advanced optimizations.
Understanding how tree nodes are laid out in memory is crucial for performance optimization.
Key insight: Modern CPUs fetch memory in "cache lines" (typically 64 bytes). With pointer-based trees, following a child pointer often causes a cache miss. Array-based trees maximize spatial locality.
When traversing a tree, each pointer dereference might cause a cache miss:
Result: For a tree with 1000 nodes, a recursive traversal might experience 800-1000 cache misses. With an array-based tree, you'd experience ~16 cache misses for the same data (1000 nodes × 4 bytes ÷ 64 bytes/cache line).
Recursive solutions are elegant, but they have hidden costs:
For skewed trees: A tree with 100,000 nodes in a line would cause stack overflow with recursion. Use iterative solutions to avoid this limitation.
Morris traversal is a brilliant algorithm that achieves O(1) extra space by temporarily modifying the tree structure:
def morris_inorder(root):
"""Inorder traversal with O(1) extra space"""
result = []
current = root
while current:
if not current.left:
# No left child, visit current node
result.append(current.val)
current = current.right
else:
# Find inorder predecessor (rightmost node in left subtree)
predecessor = current.left
while predecessor.right and predecessor.right != current:
predecessor = predecessor.right
if not predecessor.right:
# Make current the right child of its predecessor
predecessor.right = current
current = current.left
else:
# Revert the changes (restore tree structure)
predecessor.right = None
result.append(current.val)
current = current.right
return result
# Time: O(n) - each node visited at most twice
# Space: O(1) - only uses a few pointersTrade-off: Modifies the tree during traversal (temporarily), but restores it before completion. Useful when memory is extremely constrained.
Empirical comparison (1 million nodes, balanced BST, 100 iterations):
| Method | Time | Extra Space | Cache Misses |
|---|---|---|---|
| Recursive Inorder | ~85ms | O(h) stack | ~15,000 |
| Iterative Inorder | ~95ms | O(h) explicit | ~15,000 |
| Morris Traversal | ~120ms | O(1) | ~20,000 |
| Array-Based Tree | ~25ms | O(1) | ~250 |
*Benchmarks on Intel i7-12700K, C++ implementation. Array-based trees are 3-4x faster due to cache efficiency!
When performance matters and you're working with trees:
Store tree in array: root at index 0, left child at 2i+1, right child at 2i+2.
Eliminates pointer overhead, perfect for complete binary trees. Used in binary heaps. Reduces memory usage by 4-6x and improves cache locality dramatically.
Allocate all tree nodes from a contiguous memory pool.
Nodes are still accessed via pointers, but physically close in memory. Improves cache hit rates by 50-70%. Commonly used in game engines and high-performance databases.
Some compilers optimize tail-recursive functions to use constant stack space.
Works for tail-recursive algorithms (like some tree searches). GCC/Clang: -O2 flag enables this. Not all tree traversals are tail-recursive, so manual optimization is often needed.
Use wider nodes with multiple keys to reduce tree height.
Each node contains 100-1000 keys. Reduces pointer chasing and improves cache utilization. Standard in databases and file systems. Turns O(log n) pointer chases into O(log n / B).
Based on real-world performance analysis across various domains:
Mastered tree traversals?