Understanding Tree Traversals — Implementation Deep Dive
Recursive vs iterative approaches, stack-based implementations, and production-ready code for tree traversals.
Recursive vs iterative approaches, stack-based implementations, and production-ready code for tree traversals.
Author
Mr. Oz
Date
Read
8 mins
Level 2
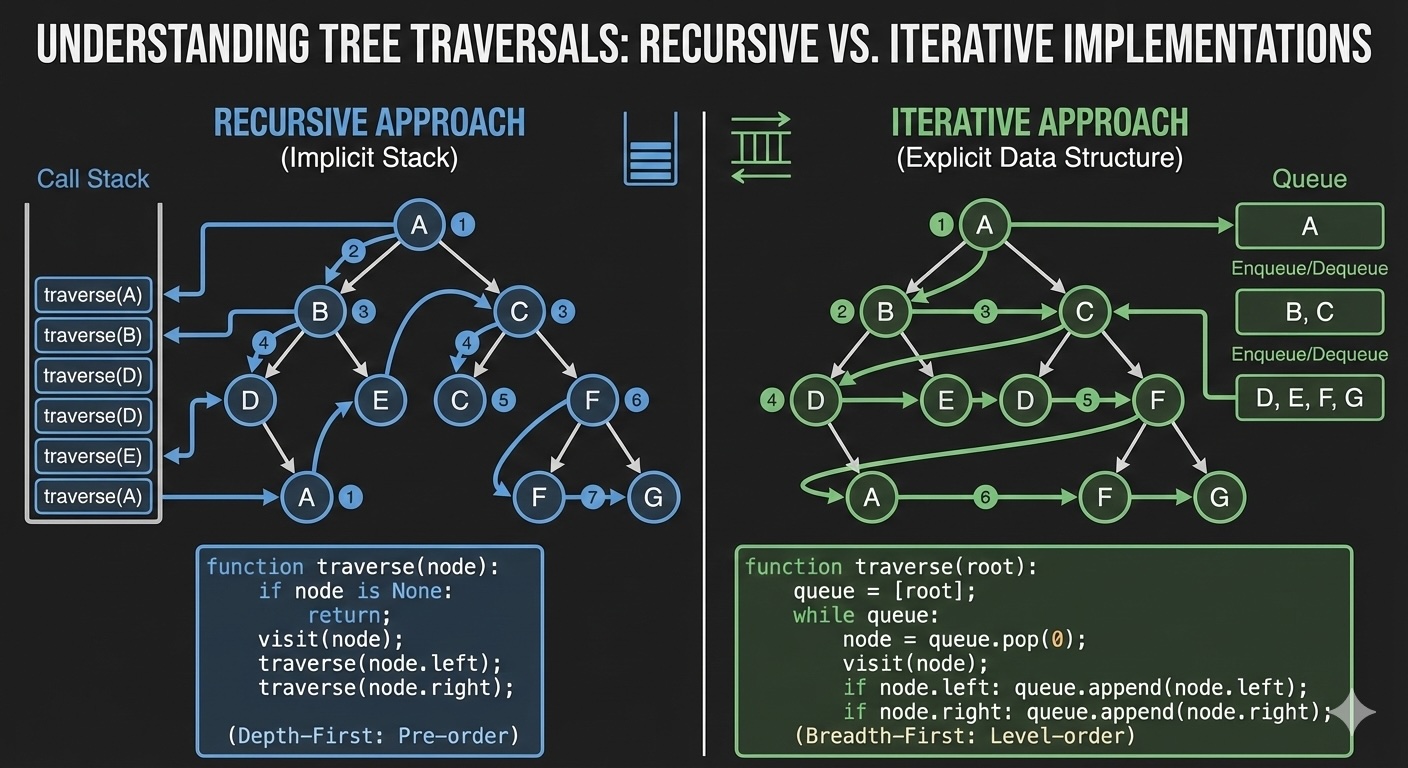
Now that we understand the library exploration analogy, let's dive into the actual implementation. We'll explore recursive solutions, iterative approaches with stacks, and production-ready patterns.
First, let's define a binary tree node. A node contains three things:
# Python implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left # Left child
self.right = right # Right child
# Java implementation
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
# C++ implementation
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};The most elegant approach — recursion naturally matches the tree structure. Each call processes a subtree.
def inorder_recursive(root):
"""Inorder traversal using recursion"""
result = []
def traverse(node):
# Base case: empty node
if not node:
return
# Step 1: Traverse left subtree
traverse(node.left)
# Step 2: Visit current node
result.append(node.val)
# Step 3: Traverse right subtree
traverse(node.right)
traverse(root)
return result
# Time Complexity: O(n) - visit each node once
# Space Complexity: O(h) - recursion stack depth, where h is tree heightKey insight: The call stack naturally remembers where to return after processing subtrees.
Visit the root first, then children. Perfect for creating a copy of the tree.
def preorder_recursive(root):
"""Preorder traversal using recursion"""
result = []
def traverse(node):
if not node:
return
# Step 1: Visit current node FIRST
result.append(node.val)
# Step 2: Traverse left subtree
traverse(node.left)
# Step 3: Traverse right subtree
traverse(node.right)
traverse(root)
return resultVisit children first, then root. Essential for deleting trees bottom-up.
def postorder_recursive(root):
"""Postorder traversal using recursion"""
result = []
def traverse(node):
if not node:
return
# Step 1: Traverse left subtree
traverse(node.left)
# Step 2: Traverse right subtree
traverse(node.right)
# Step 3: Visit current node LAST
result.append(node.val)
traverse(root)
return resultRecursion is elegant but can cause stack overflow. Let's implement iteratively using an explicit stack.
def inorder_iterative(root):
"""Inorder traversal using explicit stack"""
result = []
stack = []
current = root
while current or stack:
# Go as far left as possible
while current:
stack.append(current)
current = current.left
# Pop and visit the node
current = stack.pop()
result.append(current.val)
# Move to right subtree
current = current.right
return result
# Time Complexity: O(n) - each node pushed/popped once
# Space Complexity: O(h) - stack depth equals tree heightKey insight: The stack simulates the call stack from the recursive version.
For preorder, we push right child first (so left is processed first due to LIFO).
def preorder_iterative(root):
"""Preorder traversal using explicit stack"""
if not root:
return []
result = []
stack = [root]
while stack:
node = stack.pop()
result.append(node.val)
# Push right FIRST, then left (so left is processed first)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return resultUnlike the depth-first traversals above, this visits nodes level by level using a queue.
from collections import deque
def level_order(root):
"""Level-order traversal (BFS) using queue"""
if not root:
return []
result = []
queue = deque([root])
while queue:
node = queue.popleft()
result.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result
# Time Complexity: O(n) - visit each node once
# Space Complexity: O(w) - where w is max width of treeUse case: Finding the shortest path, level-by-level processing, or when you need to process nodes in order of depth.
if node: or if node is not None:
| Traversal | Time | Space (Recursive) | Space (Iterative) |
|---|---|---|---|
| Inorder | O(n) | O(h) | O(h) |
| Preorder | O(n) | O(h) | O(h) |
| Postorder | O(n) | O(h) | O(h) |
| Level Order | O(n) | N/A | O(w) |
Where h = tree height, w = max tree width (worst case O(n) for all)
For balanced trees, h = O(log n)
Ready for the deep dive?