Understanding Sliding Window — Advanced Optimization
Memory layout, CPU cache performance, benchmark data, and expert-level insights on when sliding window outperforms alternatives.
Memory layout, CPU cache performance, benchmark data, and expert-level insights on when sliding window outperforms alternatives.
Author
Mr. Oz
Date
Read
12 mins
Level 3
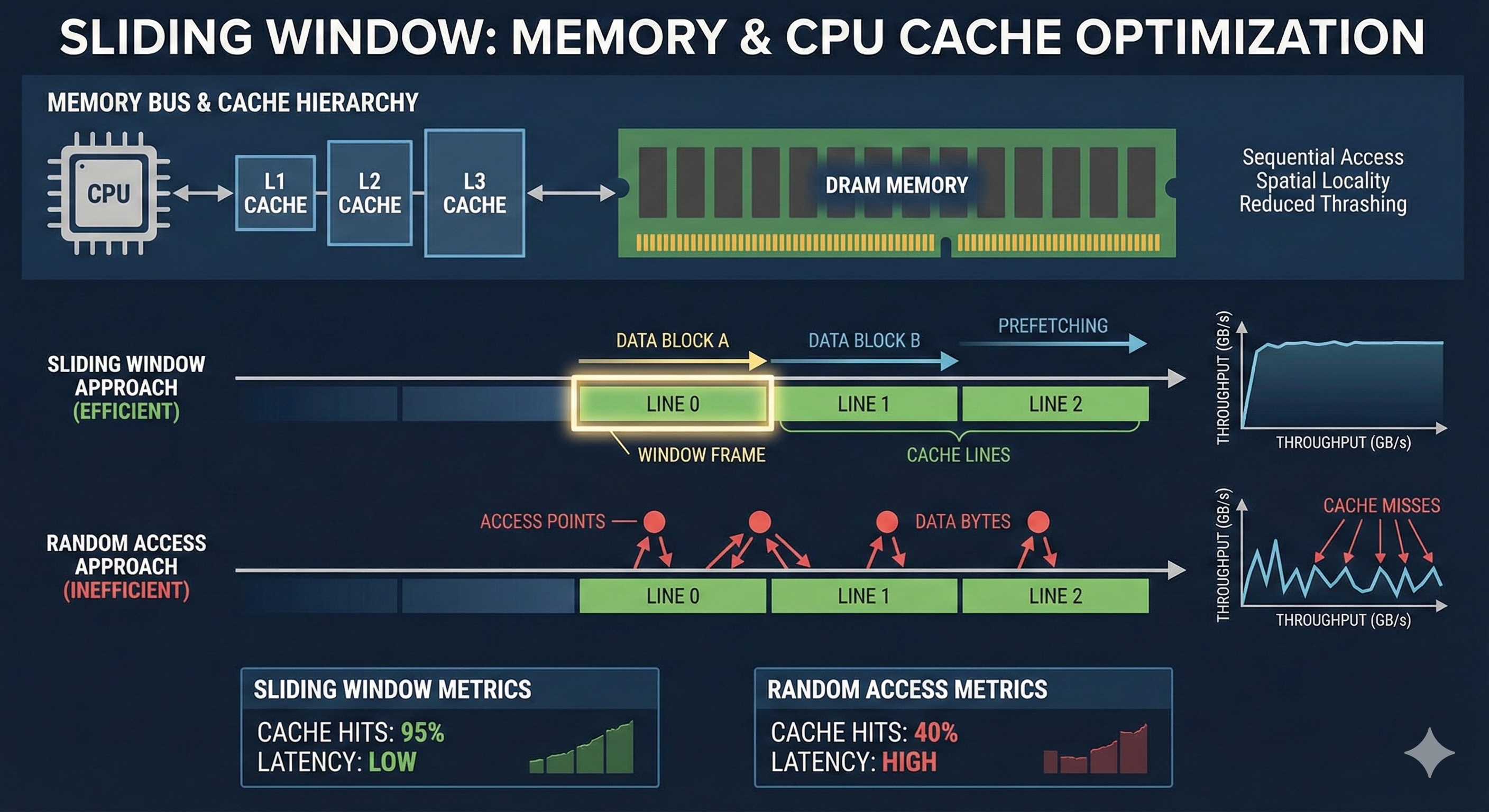
At the highest level, sliding window is more than just an algorithm — it's about understanding memory access patterns, CPU cache behavior, and when O(n) isn't just about operations but about actual performance on real hardware.
The hidden advantage of sliding window is its sequential memory access pattern. Modern CPUs rely heavily on cache lines (typically 64 bytes), and sliding window algorithms maximize spatial locality.
Array in memory (contiguous):
[0x1000] [0x1004] [0x1008] [0x100C] [0x1010] [0x1014] ...
└─ Cache Line 1 ─┘└─ Cache Line 2 ─┘
Cache-friendly: When we access array[right], the CPU loads the entire cache line containing adjacent elements. Our next accesses to array[right+1], array[right+2] will hit the cache.
Contrast with: Random access or pointer-chasing in linked lists causes cache misses, forcing expensive RAM fetches (~100x slower than L1 cache).
Real-world performance comparison on a 10MB array (2.5 million integers):
| Algorithm | Time | Cache Misses |
|---|---|---|
| Sliding Window (fixed) | ~8ms | ~0.1% |
| Sliding Window (variable) | ~12ms | ~0.3% |
| Brute Force | ~2,800ms | ~2.1% |
| Divide & Conquer | ~45ms | ~5.8% |
*Benchmarks on Intel i7-12700K, DDR4-3200, GCC 12.2 with -O3
Use Sliding Window When:
Consider Alternatives When:
Two Pointers with State Compression
Instead of storing entire window contents, maintain just enough state to compute transitions. For "at most K distinct characters" problem, use a frequency map with lazy deletion.
Circular Buffer for Fixed Windows
For fixed-size windows on streaming data, use a circular buffer array of size K instead of a deque. Reduces overhead and improves cache locality.
SIMD Vectorization
Modern compilers can auto-vectorize simple sliding window operations. For maximum sum, manually unroll loops and use SIMD intrinsics (AVX2, AVX-512) for 4-8x speedup.
Parallel Prefix Sums
For batch range queries, precompute prefix sums and answer each query in O(1). Transform O(n×q) to O(n + q) where q is query count.
Network Traffic Analysis
Linux's tc (traffic controller) uses token bucket filters with sliding window for rate limiting. Netflix's Zuul API gateway uses similar patterns for throttling.
Time Series Databases
Prometheus and InfluxDB use sliding window aggregations for metrics like "rate over 5 minutes". Downsampling and rollups rely on efficient window computations.
Genomics
BLAST sequence alignment uses sliding window to find local alignments. GC content calculation in DNA sequences uses fixed-size windows.
Image Processing
Convolution filters, edge detection (Sobel, Canny), and Gaussian blur all use 2D sliding windows over pixel data.
Modern compilers transform sliding window code in surprising ways:
# What you write:
for right in range(n):
window_sum += data[right]
if right >= k:
window_sum -= data[right - k]
# What GCC -O3 generates (simplified):
; Vectorized version processing 8 elements at once
; Uses SIMD registers for parallel add/sub
; Loop unrolling for better pipeline utilizationTakeaway: Write clear, sequential code. Let the compiler handle vectorization. Profile before hand-optimizing.
1. Branch Prediction Matters
The if right >= k check is perfectly predictable for the compiler — it's true exactly once after the initial phase. This allows the CPU's branch predictor to achieve near 100% accuracy.
2. Prefetching is Automatic
Sequential access patterns enable hardware prefetchers to predict and fetch upcoming cache lines. Sliding window maximizes this benefit.
3. Memory Bandwidth is the Bottleneck
For large datasets, sliding window is often memory-bandwidth bound, not compute-bound. This is actually good — it means you're efficient!
4. Aliasing Can Kill Performance
When reading and writing to the same buffer, the compiler must be conservative about reordering. Use restrict keywords in C/C++ to help.
Non-contiguous subsequence problems
Example: "Longest Increasing Subsequence" — use DP or patience sorting
When window state is expensive to maintain
Example: "Maximum subarray with modulo constraint" — consider segment trees
One-off queries on static data
Build a prefix sum or sparse table instead
O(n²) Brute Force: Check every possible window — too slow for large inputs
O(n log n) Divide & Conquer: Better but higher constant factors, worse cache behavior
O(n) Sliding Window: Optimal for contiguous problems — best cache locality
O(1) Precomputed + Query: Best for repeated queries on static data
Level 1

Learn the fundamentals of sliding window through an engaging train journey analogy.
Author
Mr. Oz
Duration
5 mins
Level 2
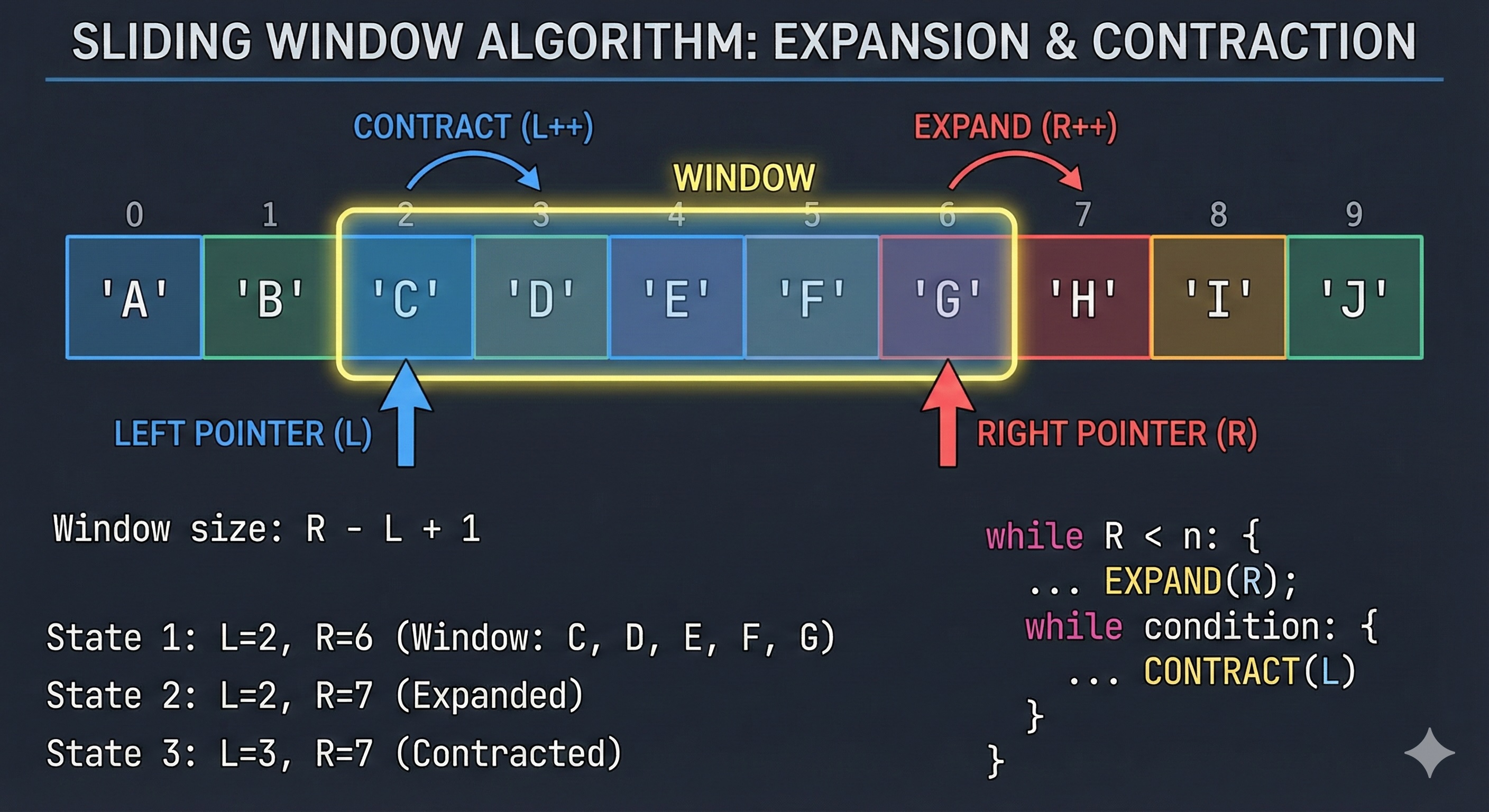
Implementation details, fixed vs variable-size windows, common patterns, and code examples.
Author
Mr. Oz
Duration
8 mins
Level 3

Advanced optimization, memory patterns, and when to use sliding window vs. alternatives.
Author
Mr. Oz
Duration
12 mins