Understanding Sliding Window — Implementation Deep Dive
Two pointer techniques, fixed vs variable-size windows, and production-ready patterns for common problems.
Two pointer techniques, fixed vs variable-size windows, and production-ready patterns for common problems.
Author
Mr. Oz
Date
Read
8 mins
Level 2
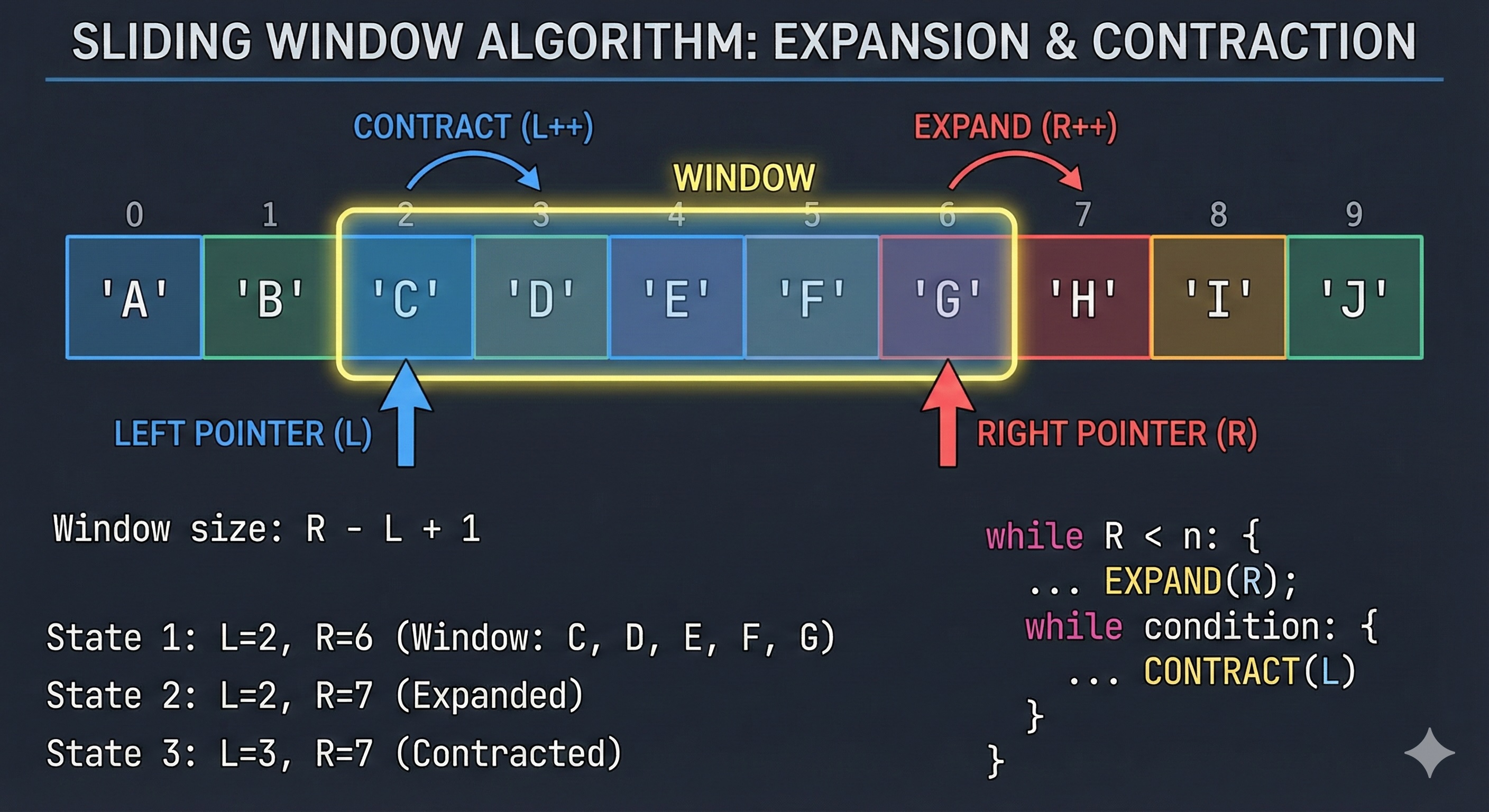
Now that we understand the train window analogy, let's dive into the actual implementation. We'll explore fixed vs variable-size windows, two pointer techniques, and how to handle edge cases like a pro.
At the heart of every sliding window solution are two pointers:
# Basic structure
left = 0
for right in range(len(data)):
# Expand window by including data[right]
# Process current window
# Shrink window from left if neededWhen the window size is known in advance, the pattern is straightforward:
# Example: Maximum sum of k consecutive elements
def max_sum_subarray(nums, k):
if len(nums) < k:
return 0
# Initialize first window
window_sum = sum(nums[:k])
max_sum = window_sum
# Slide the window
for i in range(k, len(nums)):
# Add new element, remove old element
window_sum += nums[i] - nums[i - k]
max_sum = max(max_sum, window_sum)
return max_sumKey insight: We don't recalculate the sum from scratch — we just add the new element and subtract the element we're leaving behind.
When the window grows and shrinks based on conditions, we need more careful management:
# Example: Longest substring without repeating characters
def longest_unique_substring(s):
char_map = {}
left = 0
max_len = 0
for right, char in enumerate(s):
# If char is in current window, shrink from left
if char in char_map and char_map[char] >= left:
left = char_map[char] + 1
# Update character position
char_map[char] = right
# Update maximum length
max_len = max(max_len, right - left + 1)
return max_lenKey insight: The window grows with the right pointer but only shrinks when we encounter a condition violation (like a duplicate character).
Look for these keywords and patterns:
| Operation | Time Complexity | Notes |
|---|---|---|
| Initialize window | O(k) | k = window size |
| Slide window (fixed size) | O(1) | Add new, remove old |
| Slide window (variable size) | O(1) amortized | Each element visited twice |
| Hash map lookup | O(1) average | For tracking characters/sums |
❌ Off-by-one errors
Forgetting that window size is right - left + 1, not right - left
✓ Always verify with small examples (arrays of length 1, 2, 3)
❌ Not checking if element is in current window
When shrinking, verify the element is actually within [left, right] before moving left
✓ Use map[char] >= left check before shrinking
❌ Forgetting edge cases
Empty input, single element, window size larger than array
✓ Always handle: empty array, k > len(array), k <= 0
window_start and window_end are clearer than i and jFor advanced sliding window problems like "maximum in each sliding window":
from collections import deque
def max_sliding_window(nums, k):
result = []
window = deque() # stores indices, values are in decreasing order
for i, num in enumerate(nums):
# Remove indices outside current window
while window and window[0] <= i - k:
window.popleft()
# Remove smaller elements (they can't be maximum)
while window and nums[window[-1]] < num:
window.pop()
window.append(i)
# Add maximum to result when window is fully formed
if i >= k - 1:
result.append(nums[window[0]])
return resultKey insight: The deque maintains indices in decreasing order of their values, so the maximum is always at the front.
Python
Use collections.defaultdict for frequency maps. Use enumerate() for index-value pairs.
Java
Use HashMap<K, V> for character/index tracking. Use ArrayDeque for deque operations.
C++
Use unordered_map for O(1) lookups. Use deque from <deque> for queue operations.
Ready to go deeper?
Level 1

Learn the fundamentals of sliding window through an engaging train journey analogy.
Author
Mr. Oz
Duration
5 mins
Level 2

Implementation details, fixed vs variable-size windows, common patterns, and code examples.
Author
Mr. Oz
Duration
8 mins
Level 3
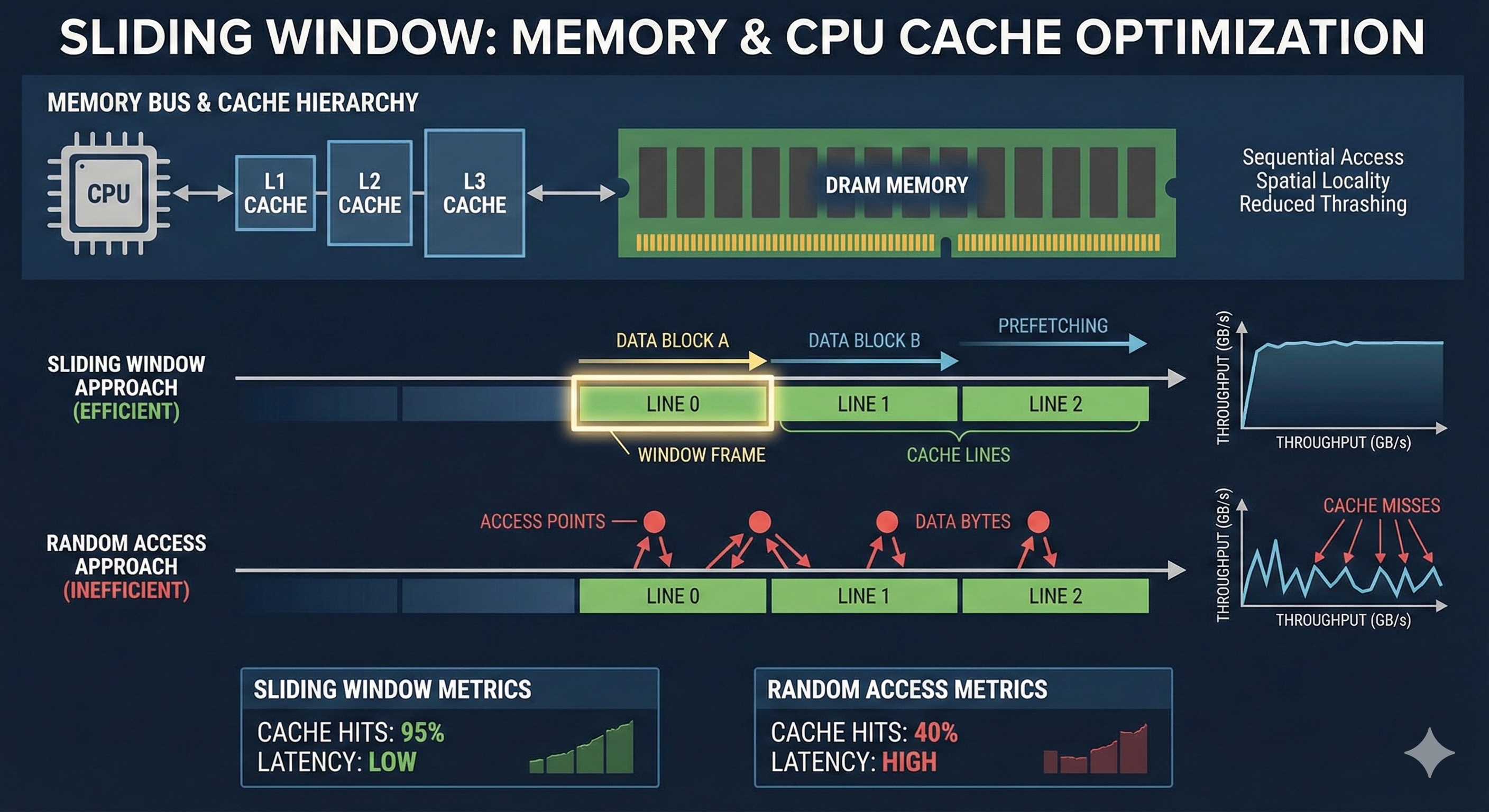
Advanced optimization, memory patterns, and when to use sliding window vs. alternatives.
Author
Mr. Oz
Duration
12 mins