Understanding Recursion: Implementation Guide
Learn to write recursive functions with proper base cases, recursive cases, and common patterns. Master the art of elegant self-referential code.
Learn to write recursive functions with proper base cases, recursive cases, and common patterns. Master the art of elegant self-referential code.
Author
Mr. Oz
Date
Read
8 mins
Level 2
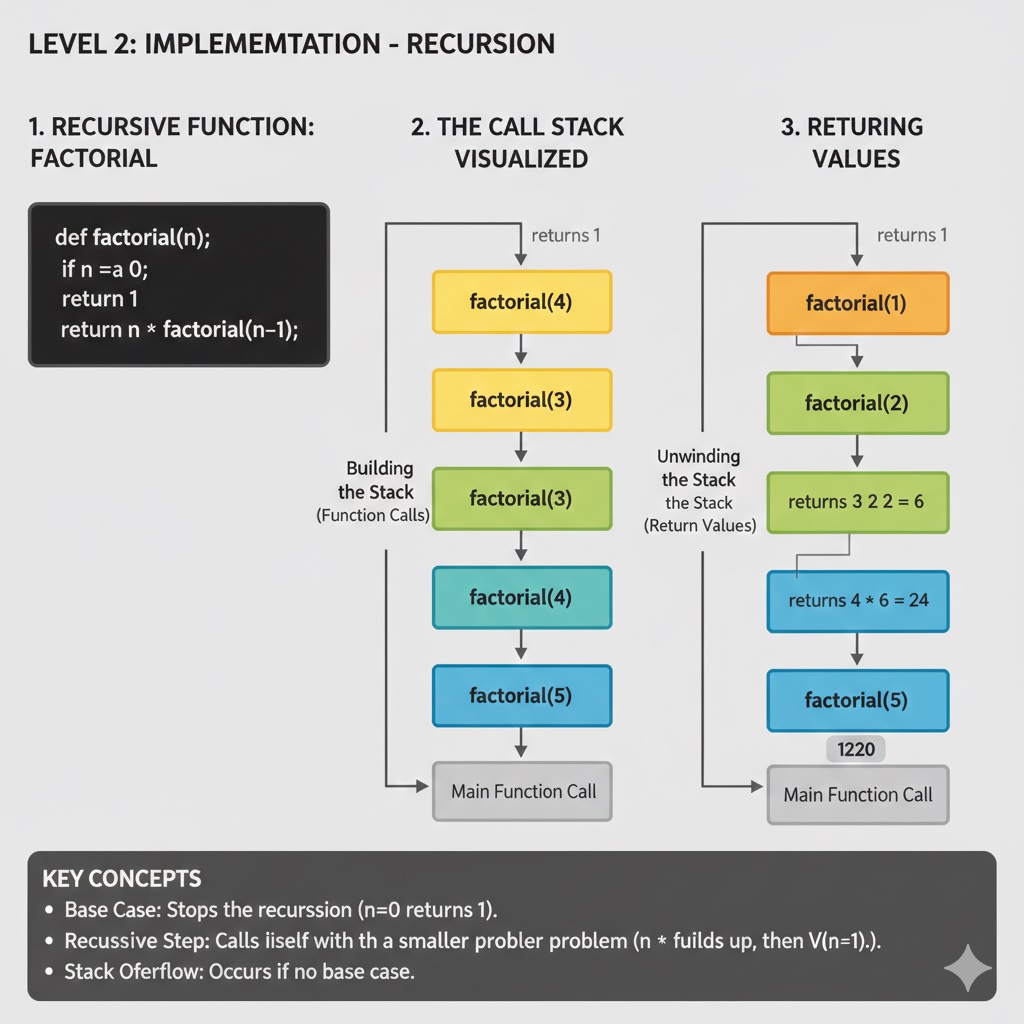
Every recursive function has two essential parts:
Without a base case, your function will call itself forever — or until the program crashes with a "stack overflow" error!
Factorial (written as n!) is the product of all positive integers up to n. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120.
Here's the recursive insight: n! = n × (n-1)!
# Python Implementation
def factorial(n):
if n <= 1: # Base case
return 1
return n * factorial(n - 1) # Recursive case
How it works:
Let's calculate the depth of a binary tree recursively:
# Python Implementation
def maxDepth(root):
if root is None: # Base case: empty tree
return 0
left = maxDepth(root.left) # Recurse on left
right = maxDepth(root.right) # Recurse on right
return 1 + max(left, right) # Combine results
This is a beautiful example because:
Here are some classic recursive problems and their patterns:
1. Linear Recursion
Function calls itself once per iteration (e.g., factorial, sum of array)
return n + recurse(n - 1)
2. Binary Recursion
Function calls itself twice per iteration (e.g., tree traversal, Fibonacci)
return recurse(left) + recurse(right)
3. Tail Recursion
Recursive call is the last operation (can be optimized by compilers)
return recurse(n - 1, accumulator)
Watch out for these mistakes when writing recursive functions:
Missing Base Case
Always include a condition that stops the recursion, or you'll get infinite calls.
Not Reducing the Problem
Each recursive call must work on a smaller version of the problem, or you'll never reach the base case.
Redundant Calculations
Naive Fibonacci recalculates the same values repeatedly. Consider memoization to cache results.
// Java - Factorial
public int factorial(int n) {
if (n <= 1) return 1; // Base case
return n * factorial(n - 1); // Recursive case
}
// C++ - Tree Depth
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0; // Base case
int left = maxDepth(root->left);
int right = maxDepth(root->right);
return 1 + max(left, right);
}
Mastered the basics?
Level 1

Learn the fundamentals of recursion through an engaging mirror room analogy.
Author
Mr. Oz
Duration
5 mins
Level 2

Implementation details, base cases, recursive cases, and common patterns.
Author
Mr. Oz
Duration
8 mins
Level 3
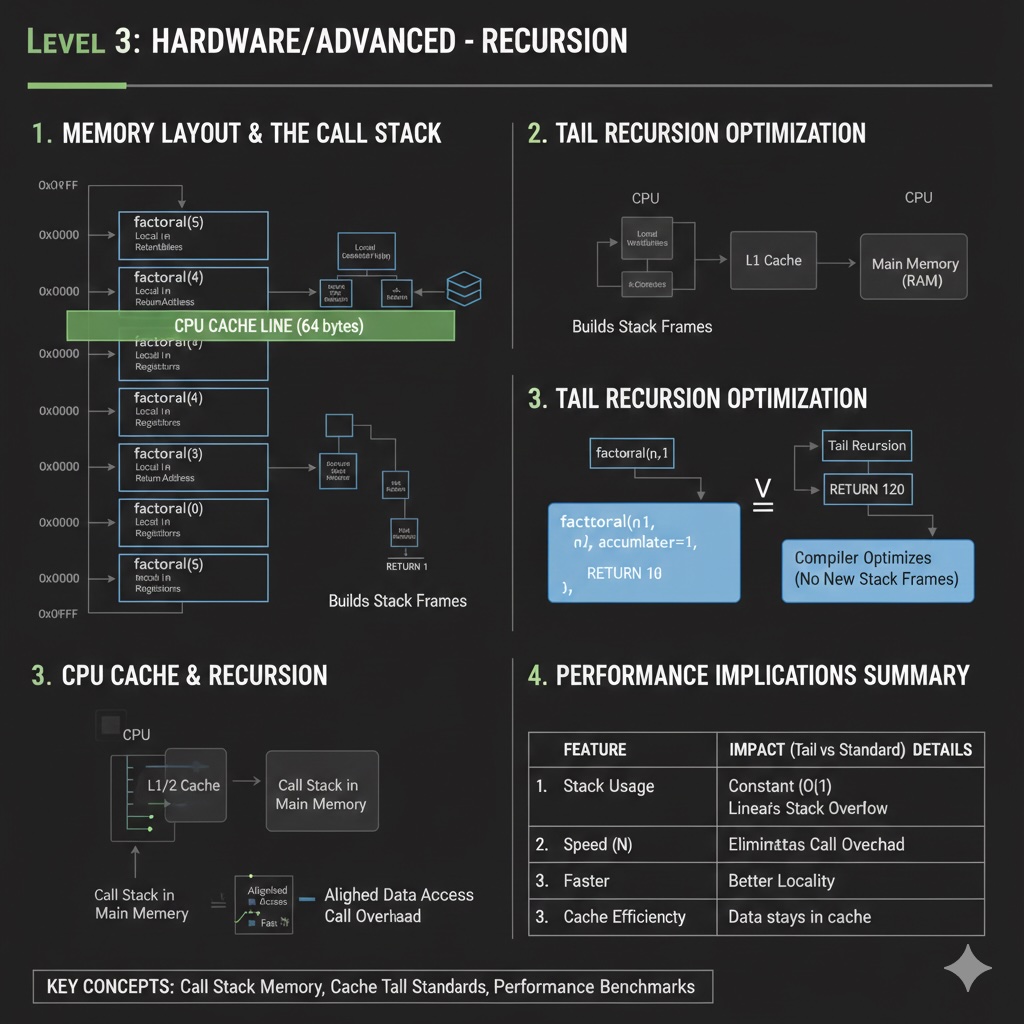
Call stack internals, tail recursion optimization, and memory considerations.
Author
Mr. Oz
Duration
12 mins