Understanding Linked Lists — Implementation Deep Dive

The Node Structure

Every linked list is built from nodes. A node contains two things:

• Value/Data: The actual content (number, string, object, etc.)
• Next pointer: Reference to the next node (or null/None if end of list)

# Python implementation
class Node:
    def __init__(self, value):
        self.value = value  # The data
        self.next = None    # Pointer to next node (initially None)

# Java implementation
class Node {
    int value;
    Node next;

    public Node(int value) {
        this.value = value;
        this.next = null;
    }
}

# C++ implementation
struct Node {
    int value;
    Node* next;

    Node(int val) : value(val), next(nullptr) {}
};

Operation 1: Traversal

The most fundamental operation — visiting each node in order. This is how we "follow the clues" in our treasure hunt.

def traverse(head):
    """Visit each node and print its value"""
    current = head  # Start at the beginning

    while current is not None:  # Continue until we reach null
        print(current.value)  # Do something with the value
        current = current.next  # Move to the next node

# Time Complexity: O(n) - we visit each node once
# Space Complexity: O(1) - we only use one pointer variable

Key insight: We never move backward — only forward. The "current" pointer advances one step at a time.

Operation 2: Insertion at Beginning

Adding a new node at the start of the list is O(1) — constant time!

def insert_at_beginning(head, value):
    """Insert a new node at the start of the list"""
    new_node = Node(value)  # Create the new node

    # Point new node's next to current head
    new_node.next = head

    # Return new node as the new head
    return new_node

# Time Complexity: O(1) - just a few pointer changes
# Space Complexity: O(1) - we only create one new node

Visual: [NEW] → [old_head] → ...

Operation 3: Insertion at End

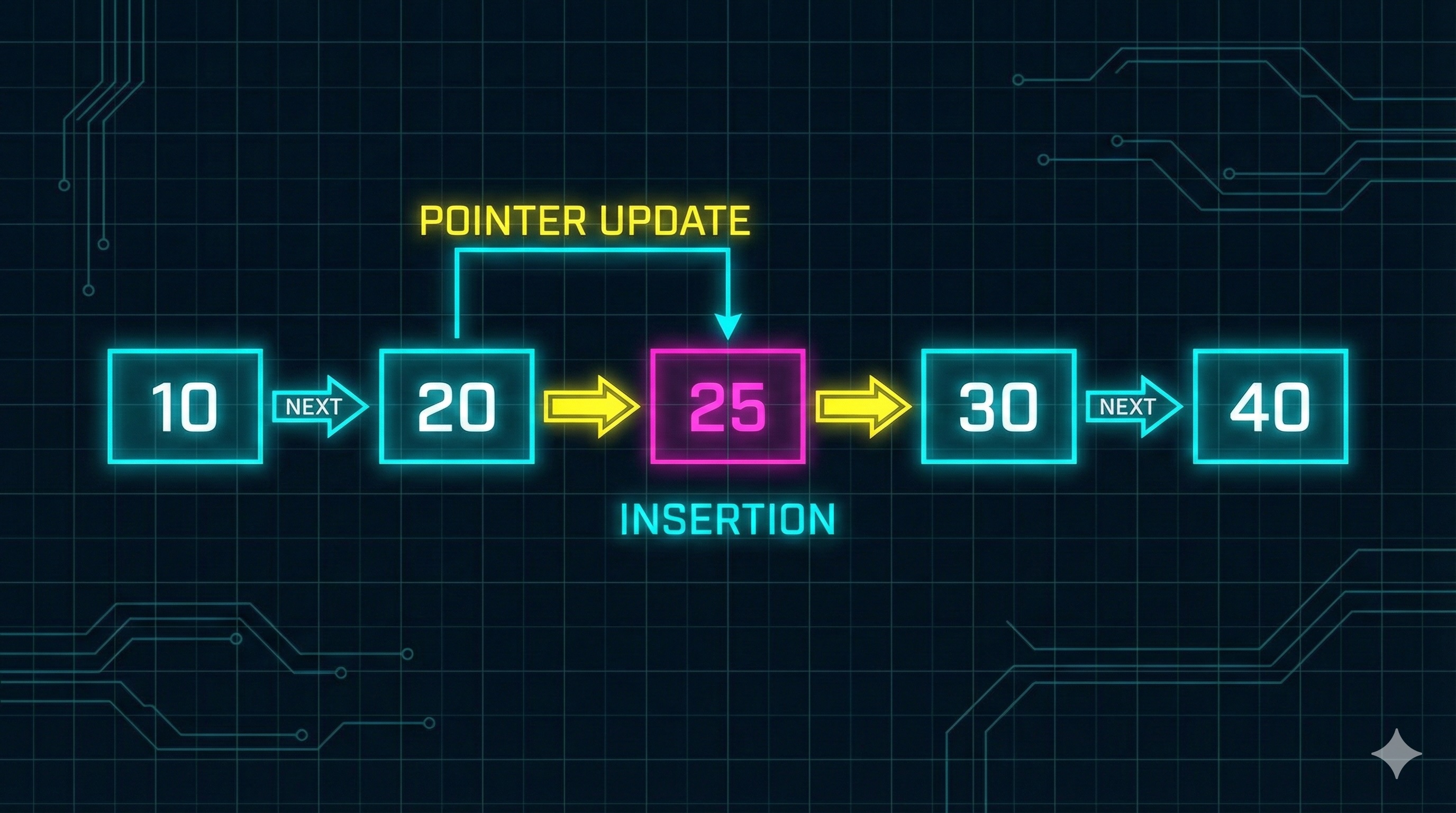
Adding at the end requires traversing to find the last node, so it's O(n).

def insert_at_end(head, value):
    """Insert a new node at the end of the list"""
    new_node = Node(value)

    # Edge case: empty list
    if head is None:
        return new_node

    # Traverse to find the last node
    current = head
    while current.next is not None:
        current = current.next

    # Attach new node
    current.next = new_node
    return head

# Time Complexity: O(n) - we must traverse to the end
# Space Complexity: O(1) - we only create one new node

Tip: If you frequently insert at the end, maintain a "tail" pointer for O(1) operations.

Operation 4: Deletion

Deleting a node requires finding the node before it, so we can redirect its pointer.

def delete_node(head, value):
    """Delete the first node with the given value"""
    # Edge case: empty list
    if head is None:
        return None

    # Edge case: deleting the head
    if head.value == value:
        return head.next

    # Find the node before the one we want to delete
    current = head
    while current.next is not None and current.next.value != value:
        current = current.next

    # If we found the node, skip over it
    if current.next is not None:
        current.next = current.next.next

    return head

# Time Complexity: O(n) - worst case, we traverse the whole list
# Space Complexity: O(1) - we only use pointer variables

Key insight: We never actually "delete" memory — we just stop referencing it. Garbage collection handles the rest (in managed languages).

The Dummy Node Pattern

One of the most elegant techniques in linked list problems is the dummy node.

Instead of worrying about which node is the "head" of our result, we create a placeholder node at the start. This eliminates special cases for the first node.

# Using dummy node to build a new list
dummy = Node(0)  # Placeholder
current = dummy

# Build the list...
current.next = Node(1)
current = current.next
current.next = Node(2)

# Return the actual result (skip the dummy)
return dummy.next

Why this matters: Without a dummy node, you'd need conditional logic to handle the first node differently. The dummy node eliminates this edge case, making your code cleaner and less bug-prone.

Common Pitfalls to Avoid

• Losing the head: Always store head.next before overwriting head pointer
  Wrong: head = head.next without saving the old head
• Null pointer dereference: Always check if node is None before accessing node.next
  Right: if node and node.next:
• Off-by-one errors: Be clear whether you're operating on current or current.next
• Memory leaks: In languages like C++, always delete nodes you remove

Time & Space Complexity Reference

*O(1) if you maintain a tail pointer