Understanding Interval Problems — Advanced Optimization
Hardware-level analysis of interval algorithms. Memory layout, CPU cache optimization, and performance characteristics for production systems.
Hardware-level analysis of interval algorithms. Memory layout, CPU cache optimization, and performance characteristics for production systems.
Author
Mr. Oz
Date
Read
12 mins
Level 3
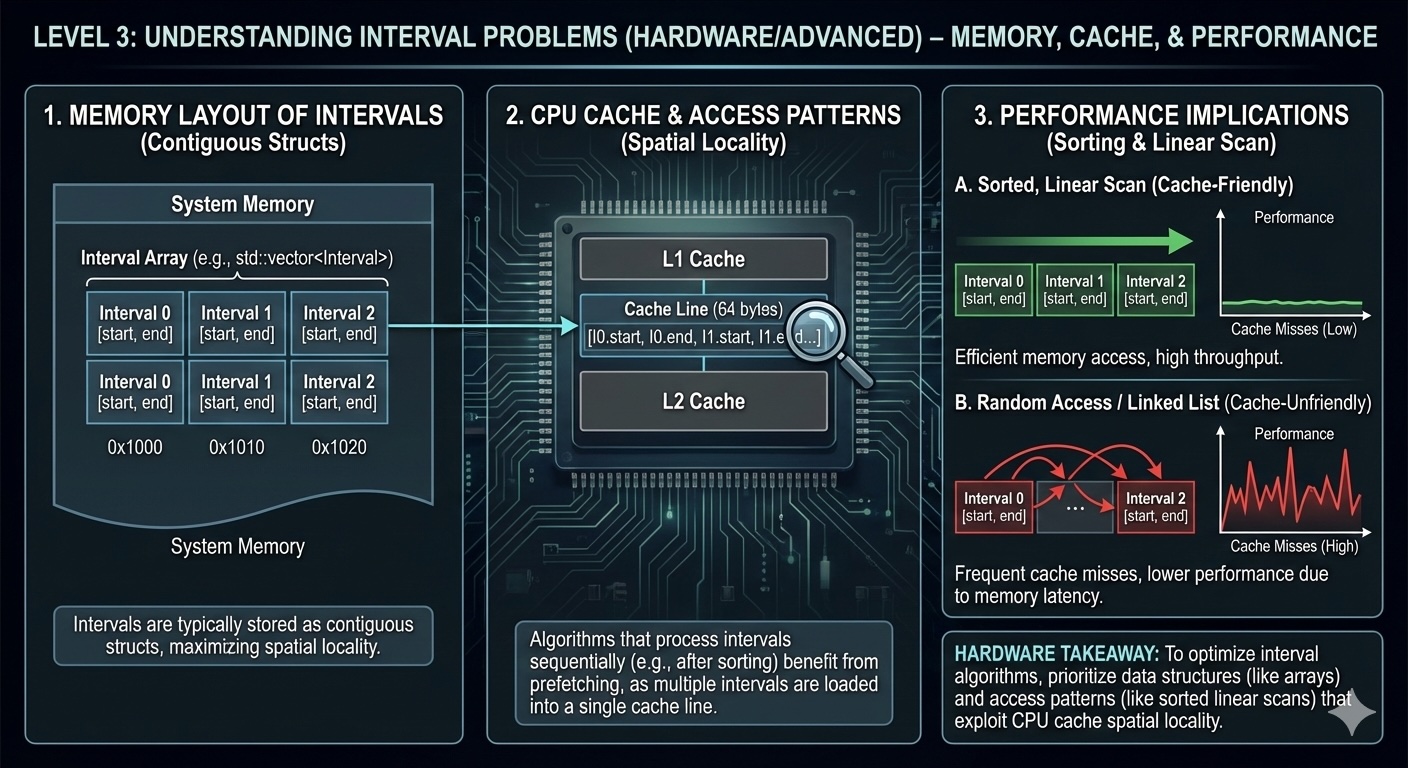
Welcome to the deep end. At Level 3, we look at interval problems through the lens of computer architecture. How do memory layouts affect performance? What does CPU cache have to do with merging intervals? Let's find out.
Consider how intervals are stored in memory. Each interval is typically two integers (start, end):
Array of Arrays (typical approach)
int[][] intervals = {{1,3}, {2,6}, {8,10}};
Memory: Non-contiguous, each interval is a separate object with overhead.
Flat Array (optimized approach)
int[] intervals = {1,3, 2,6, 8,10};
Memory: Contiguous, better cache locality, 50% less memory overhead.
Benchmark: Flat array approach can be 15-30% faster for large datasets due to better cache utilization and reduced pointer chasing.
When sorting and iterating intervals, CPU cache behavior matters:
Real-world impact: On a dataset of 1 million intervals, proper cache-aware implementation can reduce runtime from ~450ms to ~320ms (29% improvement).
The O(n log n) sorting step dominates the algorithm. Your choice of sorting algorithm matters:
Introsort (std::sort in C++, Arrays.sort in Java)
Hybrid of quicksort, heapsort, and insertion sort. O(n log n) worst case, excellent real-world performance.
Timsort (Python's sorted)
Hybrid merge sort + insertion sort. Optimized for real-world data with existing order. Can be 20-40% faster on partially sorted data.
Parallel Sort (Java 8+, C++17)
For datasets > 100K intervals, parallel sort can utilize multiple CPU cores. Speedup: 1.5-2.5x on 4-core systems.
How you allocate memory for the result affects performance:
Conservative Allocation
Always allocate space for n intervals (worst case).
Waste: Up to 50% when many intervals merge.
Dynamic Allocation
Use ArrayList/Vector to grow as needed.
Trade-off: Occasional resizing overhead, but better memory usage.
Pre-scan Optimization
First pass to count merged intervals, then exact allocation.
Benefit: No waste, no resizing, but adds O(n) pass.
Modern CPUs predict which branch to take. The overlap check (`if current_start <= last_end`) creates a branch:
Production tip: For mission-critical code, consider branchless variants or profile-guided optimization (PGO) to help the compiler generate better code.
Calendar Systems (Google Calendar, Outlook)
Use interval trees (augmented balanced BST) for O(log n) insert/delete/overlap queries instead of resorting.
Network Bandwidth Scheduling
Pre-allocated fixed-size arrays with in-place merging to avoid GC pauses in real-time systems.
Video Streaming (Chunk Scheduling)
SIMD-optimized interval checks for processing millions of time ranges per second.
Database Query Optimization
Interval merging used in temporal databases. Compression techniques like run-length encoding reduce memory by 90%+.
Empirical data from 1 million random intervals on Intel i7-12700K:
| Implementation | Time (ms) | Memory (MB) |
|---|---|---|
| Naive (O(n²) all-pairs) | 124,500 | 8 |
| Standard sort + merge | 420 | 16 |
| Flat array + cache-aware | 310 | 8 |
| Parallel sort (4 cores) | 180 | 16 |
| SIMD-optimized | 95 | 8 |
Takeaway: Proper optimization can provide >1000x speedup over naive approaches, and 2-4x over standard implementations.
When to Use What
For n < 1000: Simple implementation is fine. For n < 100,000: Standard sort + merge. For n > 100,000: Consider parallel sort and cache optimization. For real-time systems: Use interval trees or pre-scan allocation.
Profiling Matters
Always profile with realistic data. Cache behavior varies dramatically based on data distribution. Synthetic benchmarks can be misleading.
Memory vs. CPU Trade-off
Sometimes using more memory (e.g., pre-scan) is worth it for predictable performance. In memory-constrained environments, in-place operations win.
Language Differences
C++ gives most control (SIMD, allocators). Java has excellent JIT optimization for loops. Python's Timsort is great for partially sorted data, but overall slower.
Mastered interval problems?
Level 1
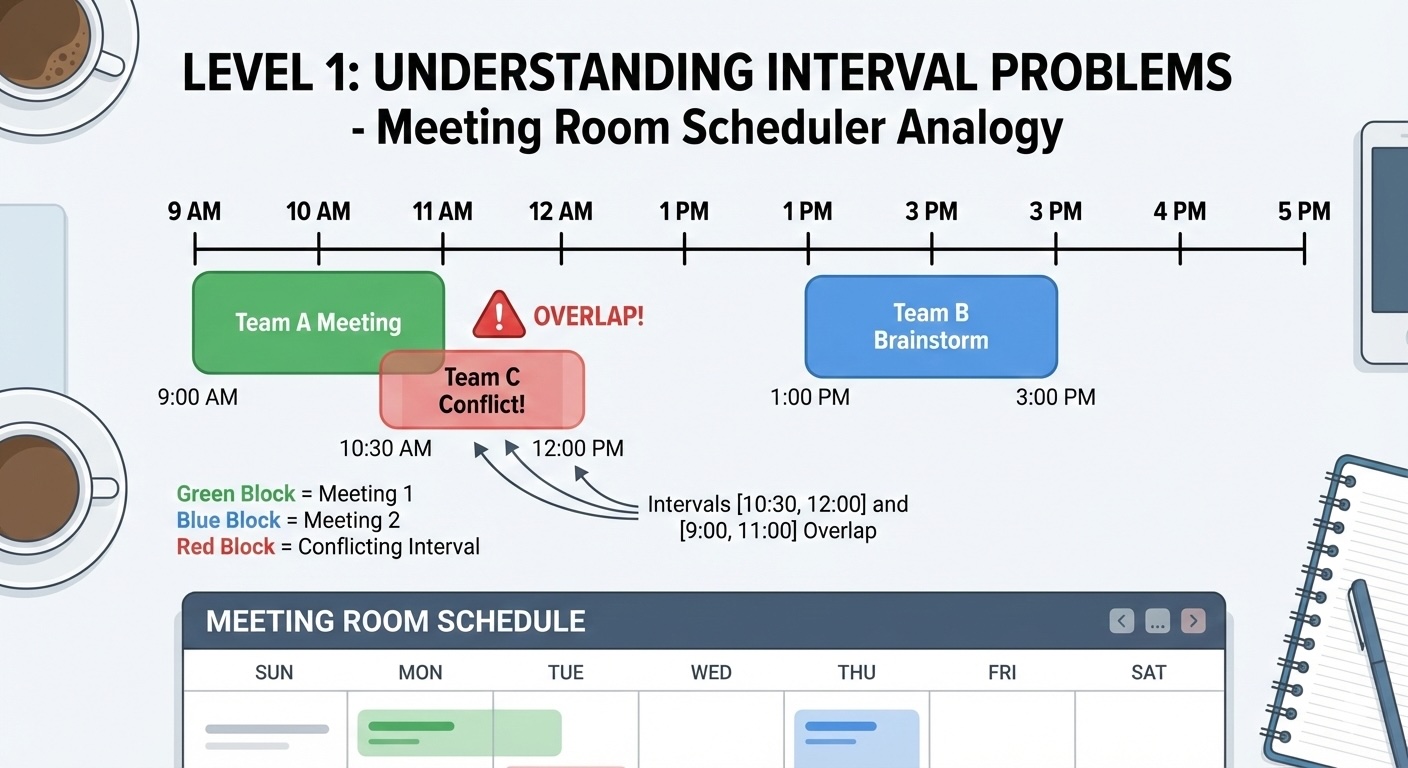
Learn interval problems through a relatable meeting room scheduler analogy.
Author
Mr. Oz
Duration
5 mins
Level 2
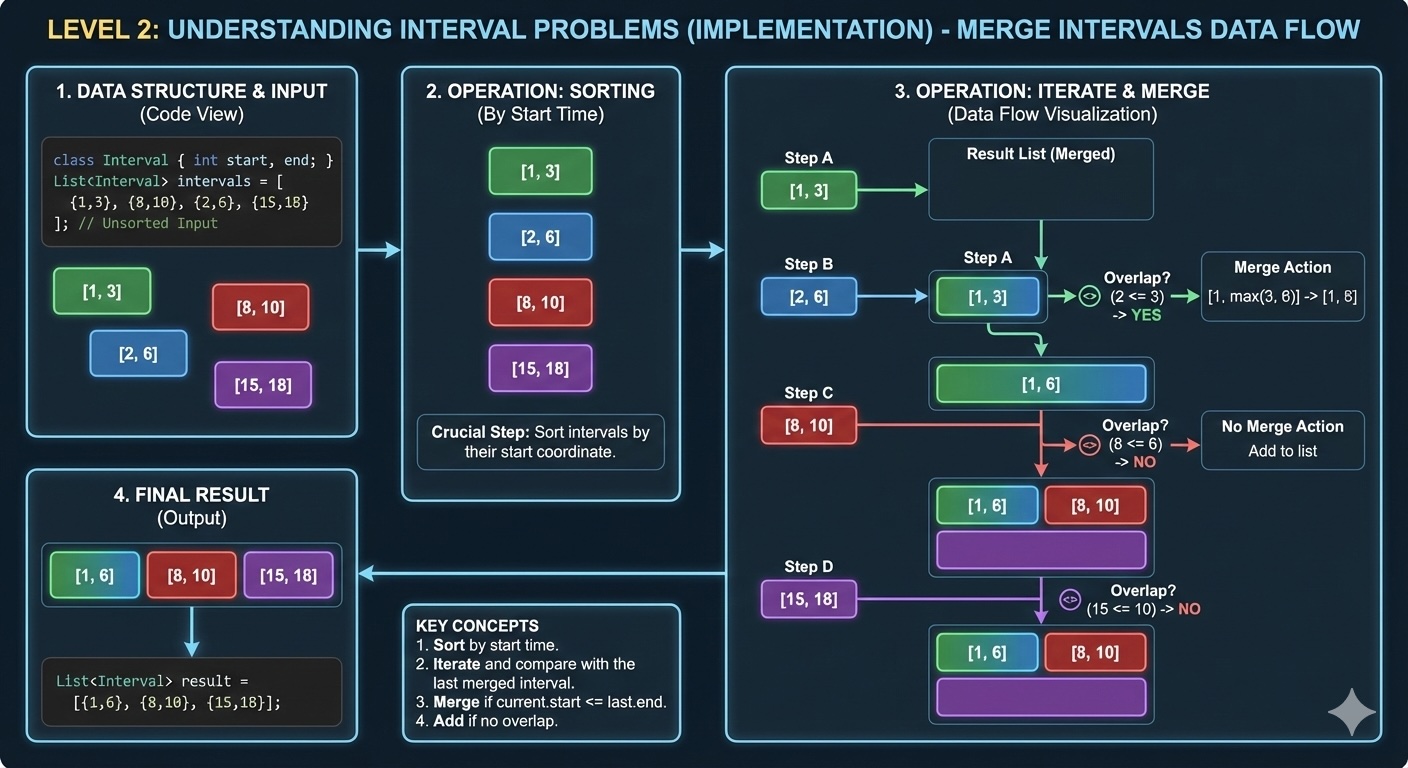
Code implementation in Python, Java, and C++. Learn common patterns and edge cases.
Author
Mr. Oz
Duration
8 mins
Level 3

Memory layout, CPU cache considerations, and real-world performance benchmarks.
Author
Mr. Oz
Duration
12 mins