Understanding Interval Problems — Implementation Guide
Code implementation in Python, Java, and C++. Learn common patterns, edge cases, and professional techniques for solving interval problems.
Code implementation in Python, Java, and C++. Learn common patterns, edge cases, and professional techniques for solving interval problems.
Author
Mr. Oz
Date
Read
8 mins
Level 2
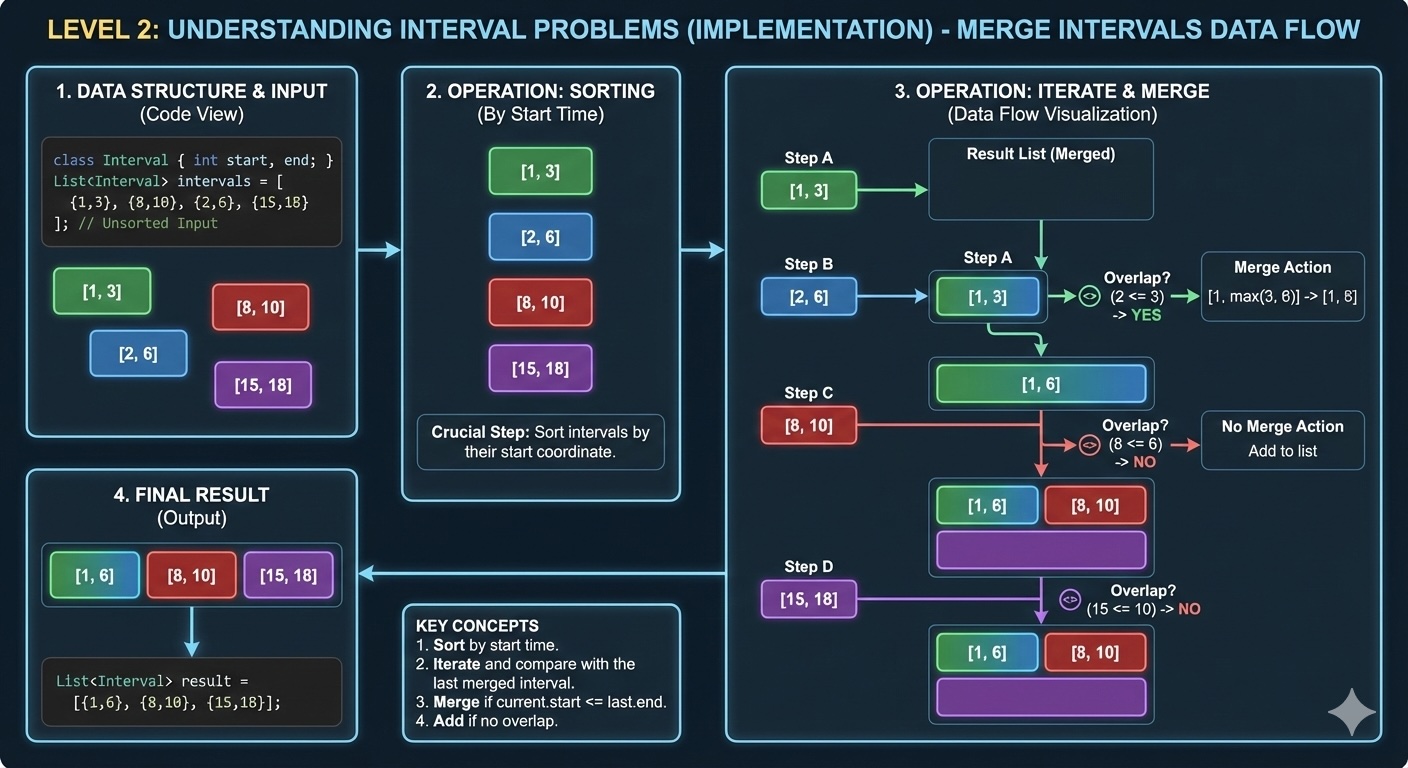
Now that you understand the concept, let's dive into the technical implementation. We'll build the merge intervals algorithm step by step, exploring code patterns and professional techniques.
Here's the step-by-step algorithm for merging intervals:
def merge_intervals(intervals):
# Edge case: empty list
if not intervals:
return []
# Sort by start time
intervals.sort(key=lambda x: x[0])
# Initialize with first interval
merged = [intervals[0]]
# Process remaining intervals
for i in range(1, len(intervals)):
current_start, current_end = intervals[i]
last_start, last_end = merged[-1]
# Check if overlap exists
if current_start <= last_end:
# Merge: update end time
merged[-1][1] = max(last_end, current_end)
else:
# No overlap: add new interval
merged.append([current_start, current_end])
return mergedKey points: Lambda function for sorting, list indexing for accessing the last merged interval, and in-place modification of the merged interval's end time.
public int[][] mergeIntervals(int[][] intervals) {
// Edge case: empty array
if (intervals == null || intervals.length == 0) {
return new int[0][];
}
// Sort by start time using comparator
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
// Use ArrayList for dynamic result
List<int[]> merged = new ArrayList<>();
merged.add(intervals[0]);
// Process remaining intervals
for (int i = 1; i < intervals.length; i++) {
int[] current = intervals[i];
int[] last = merged.get(merged.size() - 1);
// Check if overlap exists
if (current[0] <= last[1]) {
// Merge: update end time
last[1] = Math.max(last[1], current[1]);
} else {
// No overlap: add new interval
merged.add(current);
}
}
// Convert to array and return
return merged.toArray(new int[merged.size()][]);
}Key points: Lambda comparator for sorting, ArrayList for dynamic results, and array conversion at the end.
vector<vector<int>> mergeIntervals(vector<vector<int>>& intervals) {
// Edge case: empty vector
if (intervals.empty()) {
return {};
}
// Sort by start time (default vector sort)
sort(intervals.begin(), intervals.end());
// Initialize result vector
vector<vector<int>> merged;
merged.push_back(intervals[0]);
// Process remaining intervals
for (int i = 1; i < intervals.size(); i++) {
vector<int> current = intervals[i];
vector<int>& last = merged.back();
// Check if overlap exists
if (current[0] <= last[1]) {
// Merge: update end time
last[1] = max(last[1], current[1]);
} else {
// No overlap: add new interval
merged.push_back(current);
}
}
return merged;
}Key points: Reference to last interval using back(), in-place modification, and standard vector operations.
Merge Intervals
Time: O(n log n) for sorting, Space: O(n) for result
Insert Interval
Time: O(n) for linear scan, Space: O(n) for result
Interval Intersection
Time: O(n + m) two-pointer approach, Space: O(min(n, m))
Non-overlapping Intervals (Min removals)
Time: O(n log n) for sorting by end time, Space: O(1)
Forgetting to sort first
Always sort intervals by start time before processing. Without sorting, the algorithm won't work correctly.
Wrong overlap condition
Use `<=` not `<` when checking overlap. Intervals that touch at boundaries should be merged.
Not handling empty input
Always check for empty or null input at the start to avoid index errors.
Modifying input when not intended
Be aware that sorting is often in-place. If you need to preserve the original array, make a copy first.
Use Custom Comparators
In Java and C++, learn to write custom comparators for sorting by different criteria (start time, end time, length).
Separate Comparison Logic
Create helper functions like `isOverlap(a, b)` and `merge(a, b)` to make code more readable and testable.
Consider Using Classes
For production code, consider creating an `Interval` class with start, end, and helper methods instead of raw arrays.
Early Returns
Return early from functions for edge cases to reduce nesting and improve readability.
Want to understand the hardware impact?
Level 1
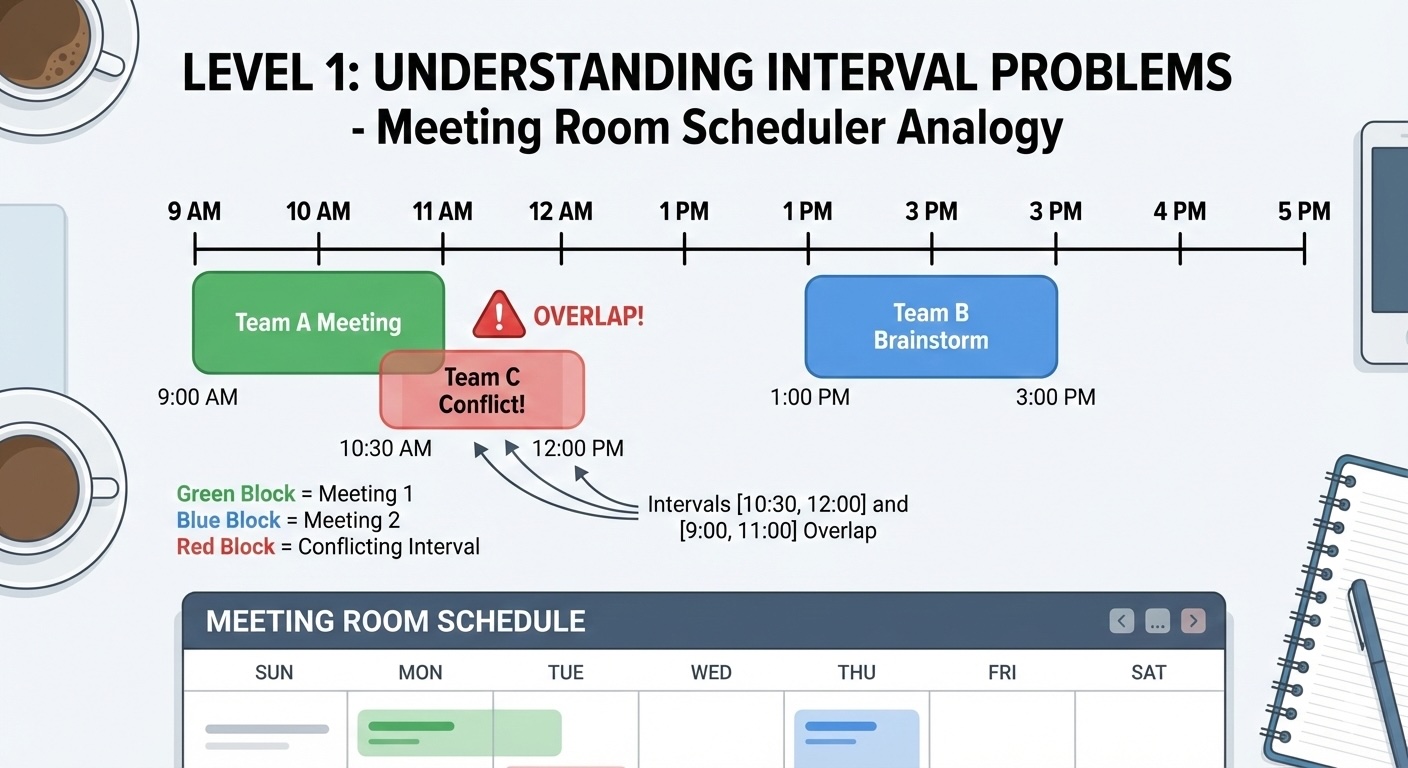
Learn interval problems through a relatable meeting room scheduler analogy.
Author
Mr. Oz
Duration
5 mins
Level 2

Code implementation in Python, Java, and C++. Learn common patterns and edge cases.
Author
Mr. Oz
Duration
8 mins
Level 3
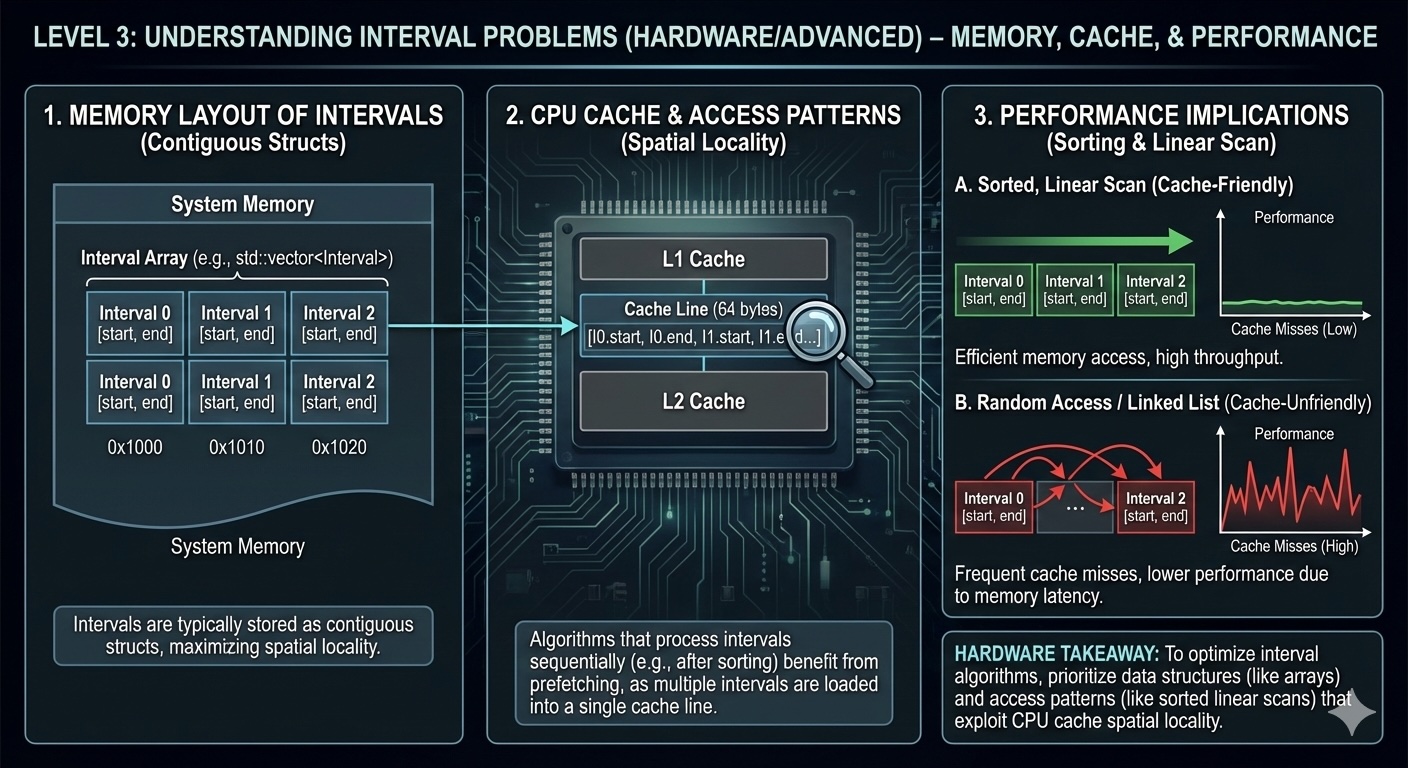
Memory layout, CPU cache considerations, and real-world performance benchmarks.
Author
Mr. Oz
Duration
12 mins