Understanding Dynamic Programming — Implementation Deep Dive
Memoization, tabulation, common DP patterns, and production-ready implementation strategies.
Memoization, tabulation, common DP patterns, and production-ready implementation strategies.
Author
Mr. Oz
Date
Read
8 mins
Level 2
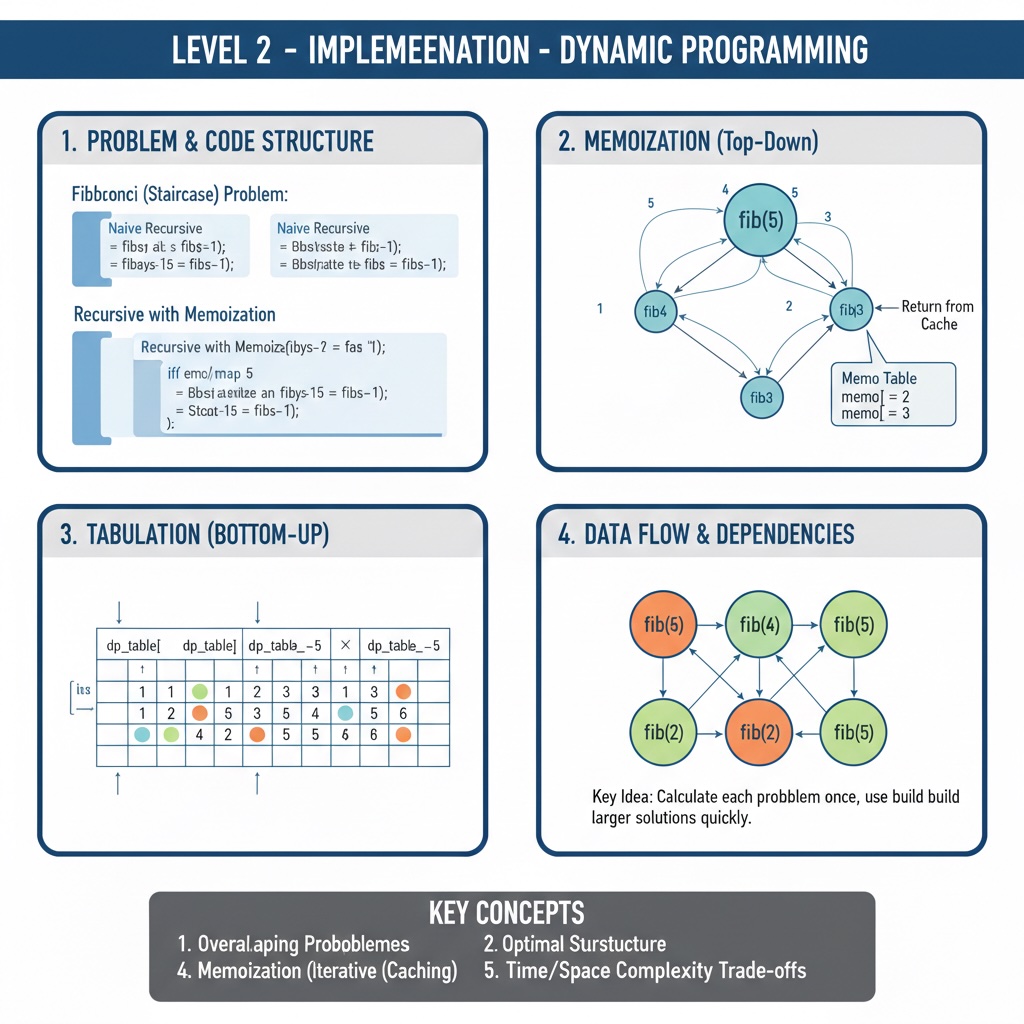
Now that we understand the staircase analogy, let's dive into the actual implementation. We'll explore memoization, tabulation, and how to build production-ready DP solutions.
There are two main ways to implement dynamic programming:
Both achieve the same result, but the approach is different. Let's see both in action!
Memoization = memo (reminder) + ization (process). It's like writing notes on your hand so you don't forget!
# Python: Top-Down with Memoization
memo = {} # Our cache
def climb_stairs(n):
if n <= 1:
return 1
if n in memo:
return memo[n]
# Calculate and store in cache
memo[n] = climb_stairs(n-1) + climb_stairs(n-2)
return memo[n]
# Usage
print(climb_stairs(10)) # Output: 89
Key insight: Before calculating, check if we already have the answer in memo!
Tabulation builds a table (array) of solutions from smallest to largest. No recursion needed!
# Python: Bottom-Up with Tabulation
def climb_stairs(n):
if n <= 1:
return 1
# Table to store solutions
dp = [0] * (n + 1)
dp[0] = 1 # Base case
dp[1] = 1 # Base case
# Fill the table
for i in range(2, n + 1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
# Usage
print(climb_stairs(10)) # Output: 89Key insight: We solve smaller subproblems first and use those results to solve larger ones.
Notice we only ever need the last two values. We can optimize to O(1) space!
# Python: Space-Optimized
def climb_stairs(n):
if n <= 1:
return 1
prev, curr = 1, 1
for i in range(2, n + 1):
prev, curr = curr, prev + curr
return curr
print(climb_stairs(10)) # Output: 89Trade-off: This uses constant space but is slightly harder to understand. Use in production!
Dynamic programming appears in many forms. Here are common patterns:
Ready for the deep dive? In the next level, we'll explore hardware-level optimizations, memory layout, and when to use DP vs other approaches.
Want to know how DP performs on real hardware? Continue to Level 3: Advanced Optimization!