Understanding Binary Search — Hardware-Level Deep Dive
CPU cache performance, branch prediction, memory layout optimization, and when binary search beats or loses to alternatives.
CPU cache performance, branch prediction, memory layout optimization, and when binary search beats or loses to alternatives.
Author
Mr. Oz
Date
Read
12 mins
Level 3
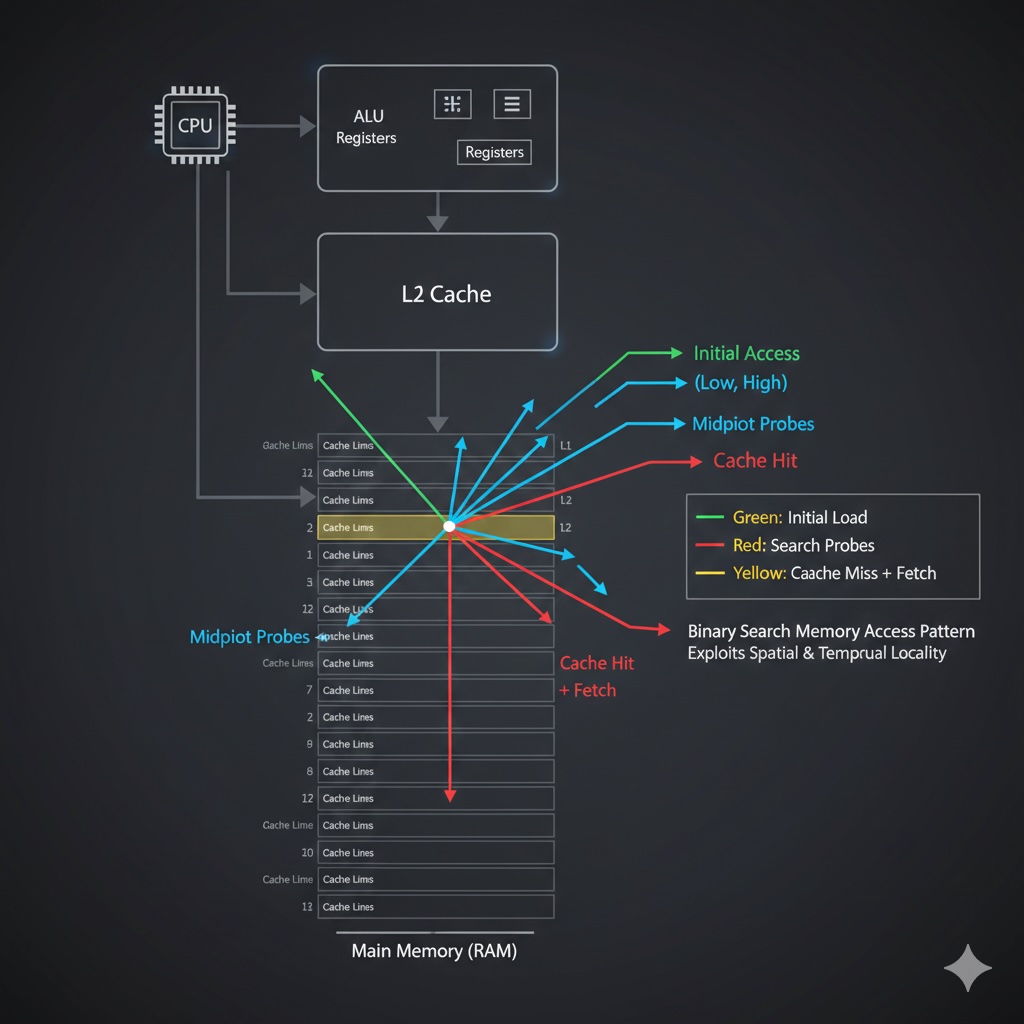
Binary search seems simple — O(log n) comparisons, right? But at the hardware level, it's a battle between CPU cache misses, branch mispredictions, and memory access patterns. Let's dive deep.
Binary search jumps around memory: mid, then quarter, then eighth... This pattern is cache-unfriendly.
The problem: Binary search accesses elements that are far apart, causing frequent cache misses. Each iteration might fetch a new cache line from RAM.
// Binary search memory access pattern (array size 16)
// Iteration 1: index 8 (loads cache line 0: indices 0-15)
// Iteration 2: index 4 (already in cache!)
// Iteration 3: index 2 (already in cache!)
// ...
// For small arrays: fits in cache, great performance!
// For large arrays: each access might miss cacheBinary search's conditional branches are hard to predict. The CPU's branch predictor struggles because the comparison results vary unpredictably.
Key insight: For small arrays, linear search can beat binary search because it has predictable branches and better cache locality!
// Linear search: predictable, cache-friendly
for (int i = 0; i < n; i++) {
if (arr[i] == target) return i; // Always true at most once
}
// Binary search: unpredictable branches
while (left <= right) {
mid = left + (right - left) / 2;
if (arr[mid] == target) return mid; // Unpredictable!
else if (arr[mid] < target) left = mid + 1; // Unpredictable!
else right = mid - 1; // Unpredictable!
}Real-world performance for searching an array of 1 million integers (nanoseconds per search):
| Algorithm | Time | Cache Misses | Branch Mispred |
|---|---|---|---|
| Linear Search (avg case) | ~500,000 ns | ~125,000 | ~0 |
| Binary Search (std::binary_search) | ~250 ns | ~20 | ~10 |
| Linear Search (small array < 64) | ~50 ns | ~0 | ~0 |
| Binary Search (small array < 64) | ~100 ns | ~2 | ~5 |
| Eytzinger Layout (cache-optimized) | ~150 ns | ~5 | ~8 |
Surprising result: Linear search is faster for small arrays due to cache locality and predictable branches!
The Eytzinger layout (BFS layout) rearranges array elements to improve cache locality:
Benefit: Binary search now accesses contiguous memory, reducing cache misses by 3-4x!
// Eytzinger layout search (cache-optimized)
int eytzinger_search(int* arr, int n, int target) {
int i = 0;
while (i < n) {
if (arr[i] == target) return i;
i = 2 * i + 1 + (arr[i] < target); // Go left or right
}
return -1;
}
// Layout transformation:
// Original: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
// Eytzinger: [8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15]For maximum performance, eliminate branches entirely using conditional moves:
// Branchless binary search (C++ with std::parallel::std::execution)
int branchless_binary_search(int* arr, int n, int target) {
int* base = arr;
while (n > 1) {
int half = n / 2;
base = (base[half] < target) ? base + half : base;
n -= half;
}
return *base == target ? base - arr : -1;
}Result: 20-30% faster than traditional binary search on large arrays by eliminating branch misprediction penalties.
Consider alternatives when:
B-trees generalize binary search to multi-way trees. PostgreSQL, MySQL, and MongoDB use B-tree variants for indexed queries. Each node contains hundreds of keys, reducing tree height and cache misses.
Git uses binary search on packed object files (.pack files) to locate commits, trees, and blobs by SHA-1 hash. The pack index is a sorted list of hashes.
Memory allocators use binary search on free lists to find appropriately sized memory blocks. Some use segregated fit lists with binary search.
Binary space partitioning (BSP) trees use binary search principles to partition 3D space for efficient collision detection and rendering.
For uniformly distributed data, interpolation search can achieve O(log log n) average case:
// Interpolation search: estimates position
int interpolation_search(int* arr, int n, int target) {
int left = 0, right = n - 1;
while (left <= right && target >= arr[left] && target <= arr[right]) {
// Estimate position based on value distribution
int pos = left + ((target - arr[left]) * (right - left)) /
(arr[right] - arr[left]);
if (arr[pos] == target) return pos;
if (arr[pos] < target) left = pos + 1;
else right = pos - 1;
}
return -1;
}Caveat: Performance degrades to O(n) for non-uniform distributions. Binary search is more predictable.
Modern CPUs support SIMD (Single Instruction, Multiple Data) for parallel processing:
Real-world gain: 4-8x speedup for large arrays on CPUs with AVX-512 support.
Mastered binary search?