Understanding Hash Tables — Implementation Deep Dive
Hash functions, collision resolution strategies, common operations, and production-ready implementation.
Hash functions, collision resolution strategies, common operations, and production-ready implementation.
Author
Mr. Oz
Date
Read
8 mins
Level 2
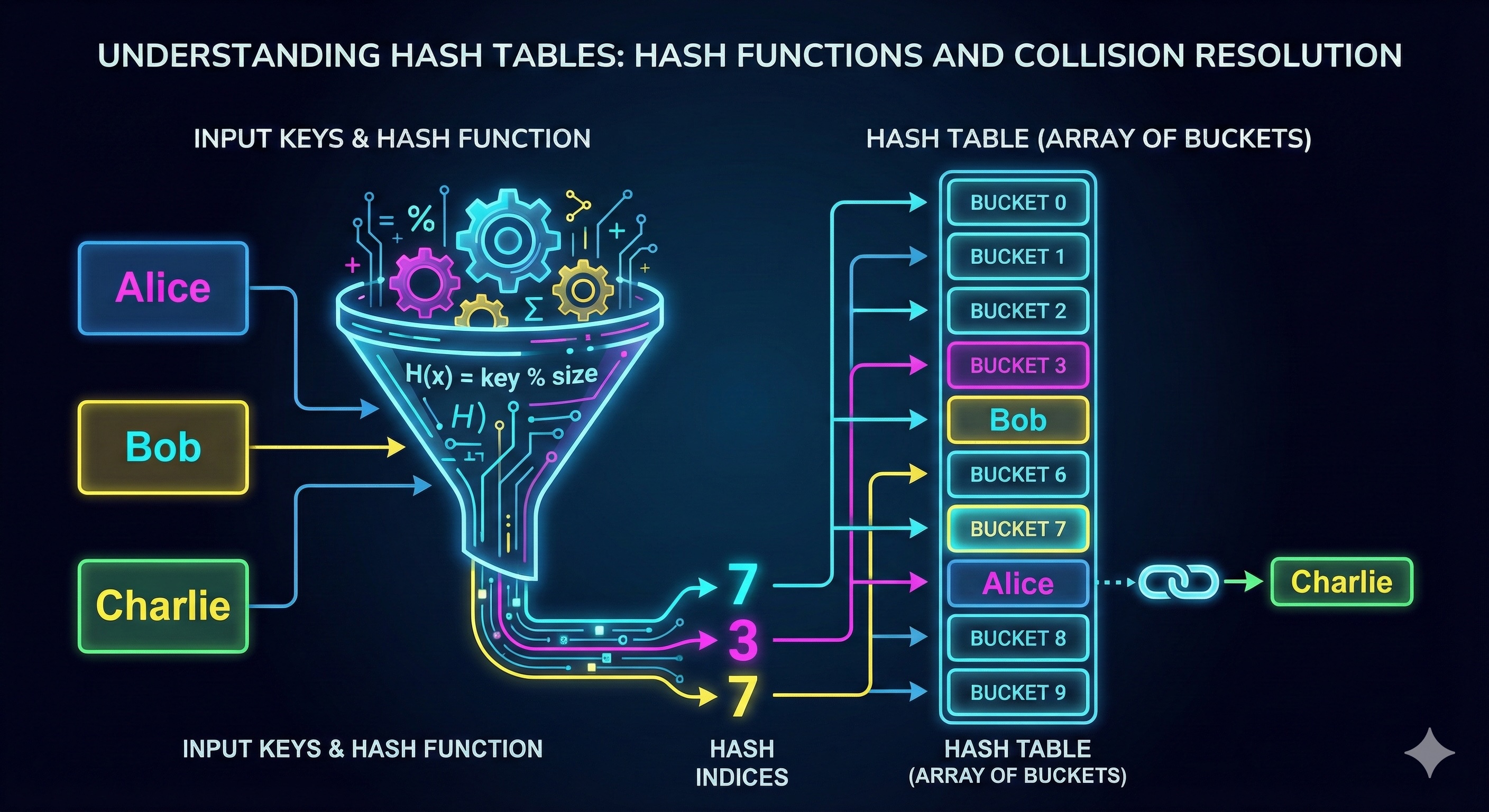
Now that we understand the magical catalog analogy, let's dive into the actual implementation. We'll explore hash functions, collision resolution, and how to build production-ready hash tables.
The hash function is the heart of a hash table. It takes a key and converts it into a bucket index.
A good hash function should:
# Simple hash function for strings
def simple_hash(key, table_size):
hash_value = 0
for char in key:
hash_value = (hash_value * 31 + ord(char)) % table_size
return hash_value
# Python's built-in hash() then modulo
def better_hash(key, table_size):
return hash(key) % table_size
# Java example
int hash = key.hashCode() % tableSize;When two keys hash to the same bucket, we have a collision. Here's how we handle it:
Each bucket contains a linked list of all key-value pairs that hash to that location.
# Visual representation
Bucket 0: []
Bucket 1: [("Alice", "555-1234")] → ("Charlie", "555-9999")
Bucket 2: [("Bob", "555-5678")]
Bucket 3: []When a collision occurs, find the next empty bucket using a probing strategy.
# Linear probing example
def put(key, value):
index = hash(key) % size
while table[index] is not None:
if table[index].key == key:
table[index].value = value # Update existing
return
index = (index + 1) % size # Move to next bucket
table[index] = KeyValue(key, value)def put(key, value):
index = hash(key) % size
# With chaining
for entry in buckets[index]:
if entry.key == key:
entry.value = value # Update
return
buckets[index].append(KeyValue(key, value)) # Insertdef get(key):
index = hash(key) % size
for entry in buckets[index]:
if entry.key == key:
return entry.value
return None # Not founddef delete(key):
index = hash(key) % size
for i, entry in enumerate(buckets[index]):
if entry.key == key:
buckets[index].pop(i) # Remove from chain
return True
return False # Not foundThe load factor is the ratio of filled buckets to total buckets:
load_factor = number_of_entries / number_of_bucketsWhen load factor exceeds a threshold (typically 0.7 or 0.75), it's time to resize the hash table!
Why resize? As the table fills up, collisions increase, performance degrades. Resizing rehashes all entries into a larger table.
Most languages provide optimized hash table implementations:
dict - Dictionary with chainingHashMap - Chaining with red-black tree for large bucketsunordered_map - Chaining implementationMap and Object - Hash table semanticsmap - Built-in hash table| Operation | Average | Worst |
|---|---|---|
| Insert | O(1) | O(n) |
| Lookup | O(1) | O(n) |
| Delete | O(1) | O(n) |
| Space | O(n) | O(n) |
Worst case occurs when all keys hash to the same bucket (degenerate to linked list). Good hash functions prevent this!
hash_map[[1,2]] = "value"
get() with default values
Ready for the deep dive?