Understanding Merge Algorithms: Implementation Guide

Dive into the technical implementation of merge algorithms. Learn the dummy node pattern, pointer manipulation, and common pitfalls to avoid.

Author

Mr. Oz

Date

1 Feb 2026

Read

8 mins

Level

The Dummy Node Pattern

When implementing merge algorithms for linked lists, the dummy node pattern is a professional technique that simplifies edge cases. Instead of treating the first node as special, we create a dummy node that serves as the starting point of our merged list.

dummy = ListNode(0)
current = dummy

This eliminates the need for special handling when the merged list is empty or when choosing which list's first node becomes the merged list's head. We always return dummy.next at the end.

Merging Linked Lists: Python Implementation

def mergeTwoLists(list1, list2):
    dummy = ListNode(0)  # Dummy node to simplify edge cases
    current = dummy

    while list1 and list2:
        if list1.val < list2.val:
            current.next = list1
            list1 = list1.next
        else:
            current.next = list2
            list2 = list2.next
        current = current.next

    # Attach remaining nodes
    current.next = list1 if list1 else list2

    return dummy.next

Merging Arrays: Python Implementation

For arrays, the approach is similar but we use indices instead of pointers:

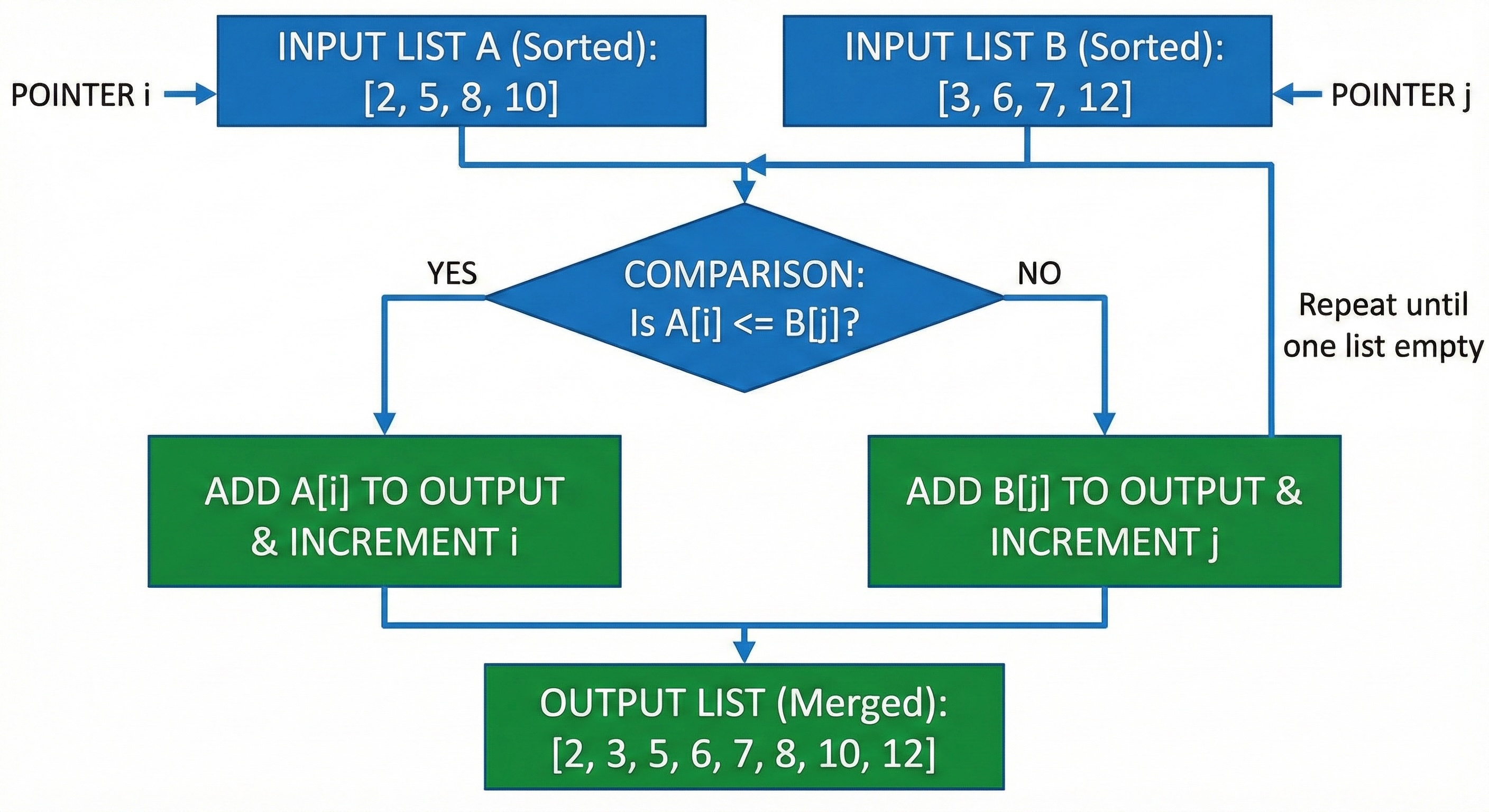
def merge_arrays(arr1, arr2):
    result = []
    i = j = 0

    while i < len(arr1) and j < len(arr2):
        if arr1[i] <= arr2[j]:
            result.append(arr1[i])
            i += 1
        else:
            result.append(arr2[j])
            j += 1

    # Add remaining elements
    result.extend(arr1[i:])
    result.extend(arr2[j:])

    return result

Common Operations and Complexities

Operation	Time Complexity	Space Complexity
Merge two sorted lists/arrays	O(n + m)	O(1) for lists, O(n + m) for arrays
Access current node	O(1)	O(1)
Append to result	O(1)	O(1)

Professional Patterns

1. Sentinel Values

The dummy node is a type of sentinel—a value that doesn't hold real data but marks boundaries. Sentinels are widely used in computer science to simplify boundary conditions.

2. In-Place Merging

When memory is constrained, you might need to merge in-place. This is trickier for linked lists but straightforward for arrays with enough buffer space.

Common Pitfalls

⚠️ Forgetting to Advance the Current Pointer

After attaching a node, always move the current pointer: current = current.next. Without this, you'll keep overwriting the same position.

💡 Modifying Original Lists

The merge algorithm modifies the next pointers of the original nodes. If you need to preserve the original lists, make copies first.

✓ Not Handling Remainder

Always attach the remaining nodes after the main loop: current.next = list1 or list2. Don't assume both lists are exhausted simultaneously.

Production Tips

Validate inputs: Check for null/empty inputs before processing
Use meaningful variable names: current is clearer than p or ptr
Document the merge strategy: Stable vs unstable merge (equal elements)
Consider recursion: Recursive solutions are elegant but may cause stack overflow for large lists

Now that you understand the implementation, let's explore the hardware-level optimizations and real-world performance considerations in Level 3.