Palindrome Number — Level 3

To understand why the mathematical approach is superior, we have to look at the CPU and JVM internals. This is where theory meets silicon.

1. The Cost of Division vs. Branching

   In our code, we use x % 10 and x / 10. Historically, division is one of the "slowest" instructions on a CPU compared to addition or bit-shifting.

   However, modern compilers and JIT (Just-In-Time) optimization are incredibly smart. When you divide by a constant (like 10), the compiler often replaces the DIV instruction with a "Reciprocal Multiplication."

   How it works: Instead of dividing, the CPU multiplies by a specific "magic number" and then shifts the bits. This is significantly faster than a standard division instruction.

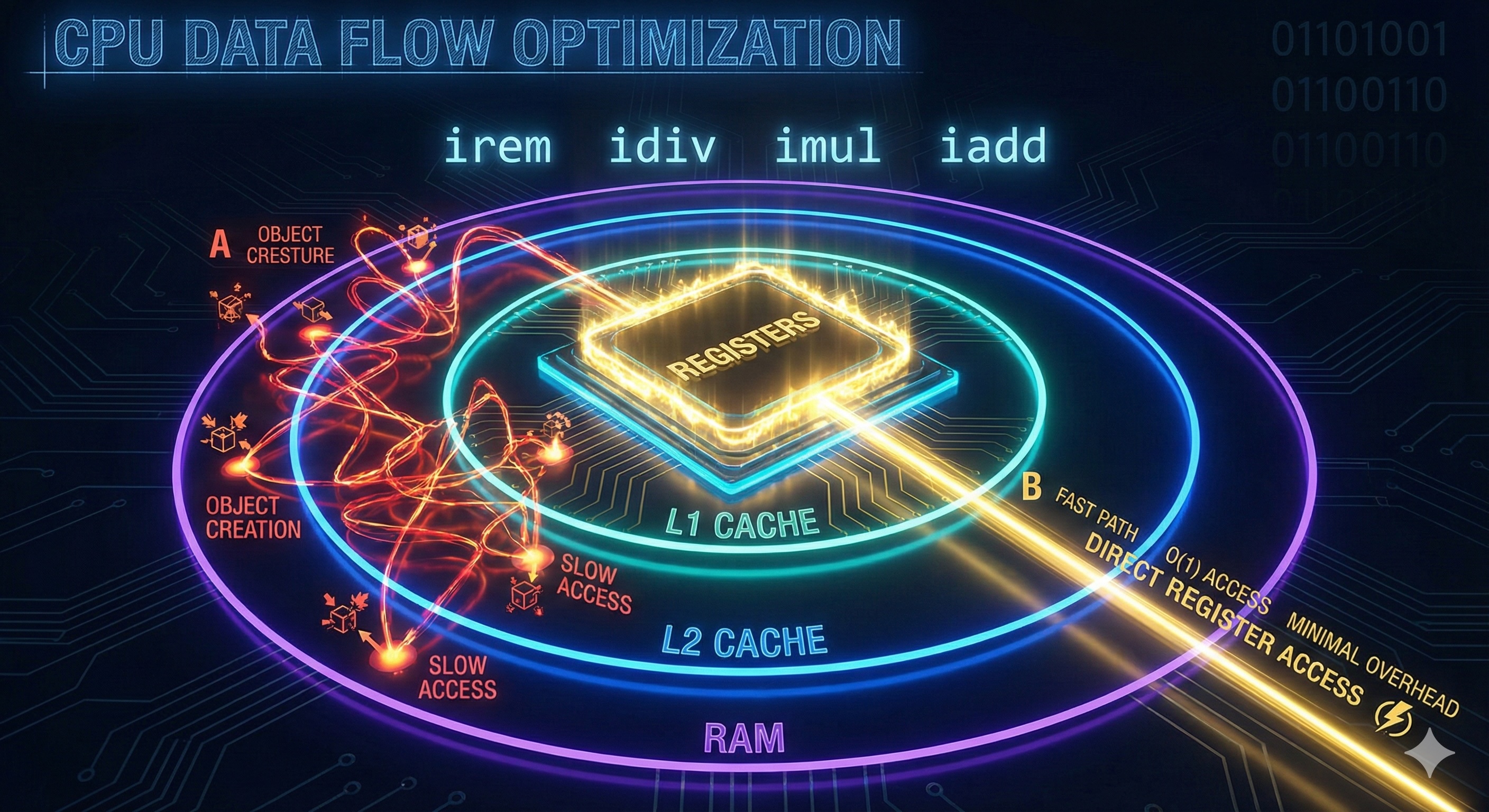
2. CPU Cache and Locality

   When you use the mathematical approach, all your data fits in CPU Registers. Registers are the fastest storage in the computer (sub-nanosecond access).

   Storage Level	Access Time	Used By
   CPU Registers	~0.5 ns	Math approach
   L1 Cache	~1-2 ns	Small objects
   L2 Cache	~4-7 ns	Medium objects
   Main RAM	~100 ns	String approach

   When you convert to a String, the data moves to the L1/L2 Cache or even the Main RAM. Accessing RAM can be 100x to 200x slower than accessing a register. By staying in "Math land," you keep the data as close to the "brain" of the computer as possible.

3. Branch Prediction

   The while (x > revertedNumber) loop is very "predictable" for a CPU's branch predictor.

   The CPU guesses that the loop will continue and starts pre-fetching the next instructions. Because the logic is simple and doesn't involve complex object lookups, the "pipeline" stays full.

   Why this matters: Modern CPUs execute instructions in a pipeline. A mispredicted branch can cause a "pipeline flush" — throwing away 10-20 cycles of work. Simple, predictable loops avoid this penalty.

4. Immutability and Bytecode

   If you look at the Java Bytecode (javap -c), the String approach involves many expensive operations:

   // String approach bytecode (simplified)
   invokestatic  Integer.toString    // Create string from int
   new           StringBuilder       // Allocate new object
   invokespecial <init>              // Constructor call
   invokevirtual reverse             // Method dispatch
   invokevirtual toString            // Another allocation
   invokevirtual equals              // Comparison

   Our mathematical approach translates to simple, fast instructions:

   // Math approach bytecode (simplified)
   irem    // Integer remainder (x % 10)
   idiv    // Integer division (x / 10)  
   imul    // Integer multiplication (* 10)
   iadd    // Integer addition

   These are the bread and butter of the JVM. They require no method dispatch overhead and can be easily inlined by the JIT compiler.

5. The Data Path Visualization

   Think of it this way:

   String Approach Path

   Integer → Heap (String) → Array (char[]) → Heap (StringBuilder) → Array (char[]) → Heap (new String) → Comparison

   Multiple memory allocations, cache misses likely

   Math Approach Path

   Register → Register → Register → Comparison

   All in registers, zero allocations