Palindrome Number — Level 2
A developer-focused deep dive into palindrome checking in production.
Learn about Integer Overflow,
Memory Pressure, and why the "Half-Reversal" strategy is professional-grade.
A developer-focused deep dive into palindrome checking in production.
Learn about Integer Overflow,
Memory Pressure, and why the "Half-Reversal" strategy is professional-grade.
Author
Mr. Oz
Date
Read
8 mins
Level 2
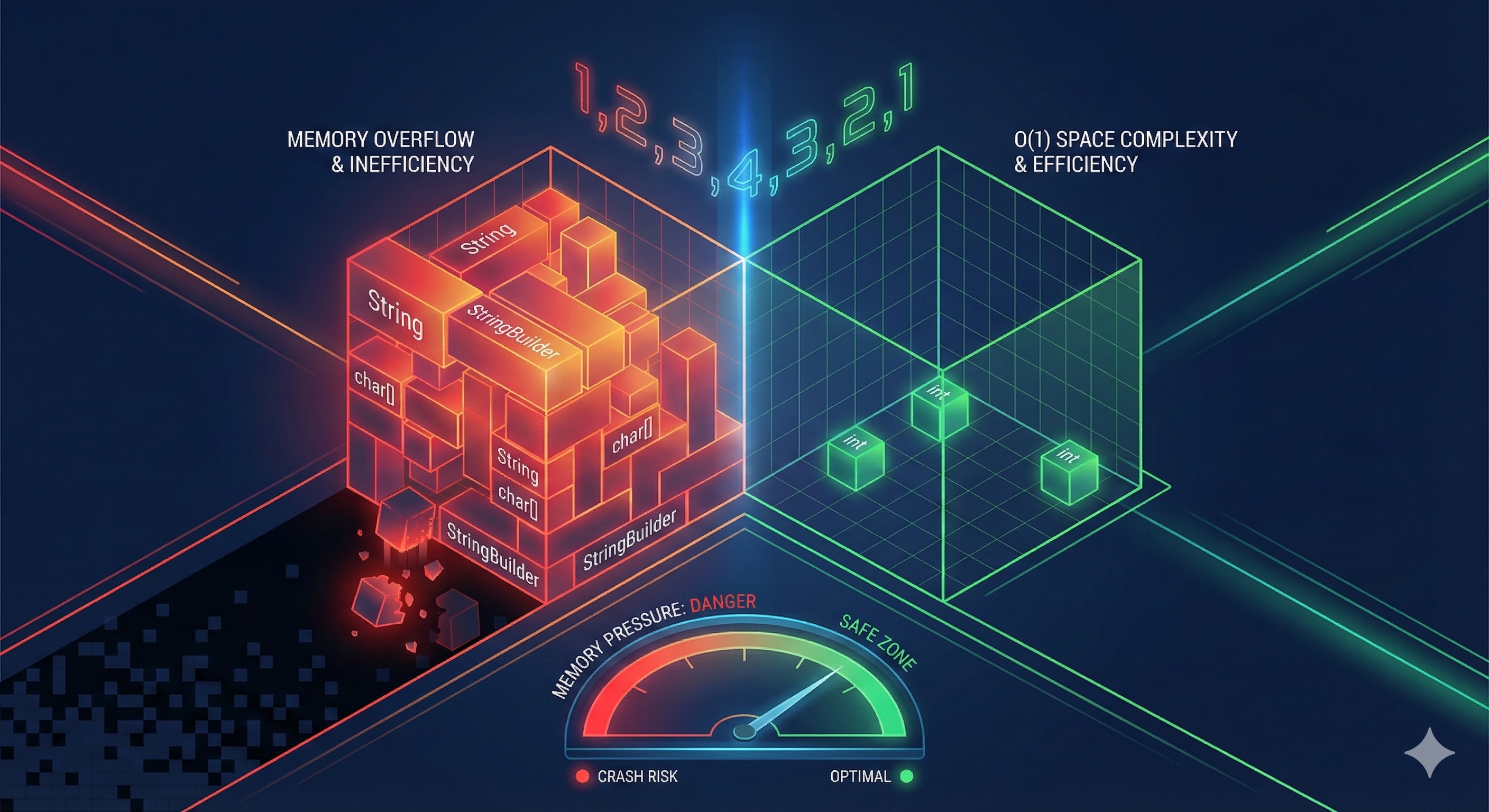
In a production environment, Palindrome Number is rarely about the "Reverse a String" trick. Interviewers use this problem to see if you understand Integer Overflow and Memory Pressure.
There are three main reasons why converting to a String is problematic in production:
Integer.toString(n) creates a new String object.
Strings are immutable in Java. This lands on the Heap.
If you are running this check inside a loop processing millions of transactions per second (like a high-frequency trading bot or a sensor data aggregator), you are creating millions of short-lived objects. The Garbage Collector (GC) will eventually have to "Stop the World" to clean them up, causing latency spikes.
A String is backed by a byte[] or char[].
There is header overhead for the object and the array length.
The most robust way is reversing only half of the integer. But why half?
Because if you reverse a 32-bit integer completely, the reversed version might exceed
2,147,483,647 (the max value of a 32-bit signed int).
By stopping at the middle, we guarantee the number stays within the bounds of a standard int.
public boolean isPalindrome(int x) {
// Negative numbers are not palindromes
// Numbers ending in 0 (except 0 itself) are not palindromes
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// For even-length: x == revertedNumber
// For odd-length: x == revertedNumber / 10 (middle digit ignored)
return x == revertedNumber || x == revertedNumber / 10;
}This is incredibly fast. For a 10-digit number (the max for a 32-bit int), the loop only runs about 5-10 times.
This is the "holy grail." It means the memory usage is constant regardless of how big the number is.
On a mobile device with limited RAM or an embedded system (like a smart fridge), this is the difference between a smooth app and a crash.
false (the minus sign breaks symmetry)Integer Overflow.long if you need to handle larger numbers.Want to go deeper?
Continue to Level 3: CPU Internals, Cache, and Bytecode